Obsah
Případové studie
Tato kapitola je součástí práce Alternativní jednoduché modely podzemní vody
Využití alternativních jednoduchých modelů je demonstrováno na případových studiích. Případové studie jsou v terénním měřítku a jsou sadou jednoduchých modelů, či srovnáním jednoduchého modelu s modelem komplexním. Případové studie byly zpracovány většinou s malým množstvím adekvátních dat, a umožňují tak testovat „hloubku naší neznalosti“ – epistemologickou nejistotu. Vzhledem k tomu, že modely jsou často prediktivní a není nedostatek dat pro srovnání s výsledky modelu, jednotlivé modely nejsou mezi sebou srovnávány matematickými a statistickými metodami, ale nejistotu vyjadřují víceméně rozmezím hodnot. Modely byly většinou sestaveny pro analýzu rizika v rámci komerčních zakázek. Tabulka 7 aplikuje Klasifikaci využití modelů na případové studie.
Tabulka 7: Aplikace Klasifikace využití modelů na případové studie
| Různé | Lokalita | Smědá | Jez | Luštěnice | Vikýř. | Hořice |
|---|---|---|---|---|---|---|
| Interpretační model | ✔ | ✔ | ✔ | |||
| Testování hypotéz | ✔ | ✔ | ||||
| Vztah model–událost (jev) | Proof of concept | |||||
| Inverzní model | ✔ | ✔ | ||||
| Hodnocení vlivu očekávaných změn | Analýza citlivosti | |||||
| Scénáře | ||||||
| Předpovědi budoucnosti | Ex-post forecasting | ✔ | ||||
| Ex-ante forecasting | ✔ | |||||
| Analýza nejistoty | ✔ | |||||
| Analýza citlivosti | ||||||
| Neparametrický výpočet | ||||||
Ekvifinalita – interakce povrchové a podzemní vody
První studie je pravděpodobně nejnázornější aplikace principu ekvifinality a testování hypotéz ze všech případových studií (Skořepa et al. 2009). Nejedná se totiž o predikce, ale o vysvětlení pozorovaného stavu.
V toku Smědá ve Frýdlantském výběžku dochází ke ztrátám průtoku (m3/s). Za léta 1995–2008 byla ve 24 měsících (40 % ztrátových měsíců) ztráta statisticky významná (větší než 10 %). Mezi stanicí ČHMÚ Višňová a Předlánce (tj. v mezipovodí I) se projevovala ztráta výjimečně, ale mezi stanicemi Předlánce a Ostrožno (tj. v mezipovodí II) se ztráta projevovala za posledních 9 let ve 40 % sledovaných měsíců. Průměrná ztráta (pokud se projeví) je v mezipovodí II cca 240 l/s. Ztráta se projevuje zejména při nízkých průtocích. Ke ztrátě může docházet i v měsících, kdy po směru toku průtok narůstá. Hodnocení totiž nepracuje s ostatními přítoky Smědé (drobné vodoteče, povrchový a podpovrchový odtok).
Je možno zformulovat několik hypotéz (obrázek 11), kam se voda ze Smědé ztrácí. Některé hypotézy jsou dále testovány matematickým modelem. Všechny modely byly představovány jednoduchými vzorci, které jsou založeny na Darcyho zákonu a rovnici kontinuity. Modely byly vypočítány v MS Excel.
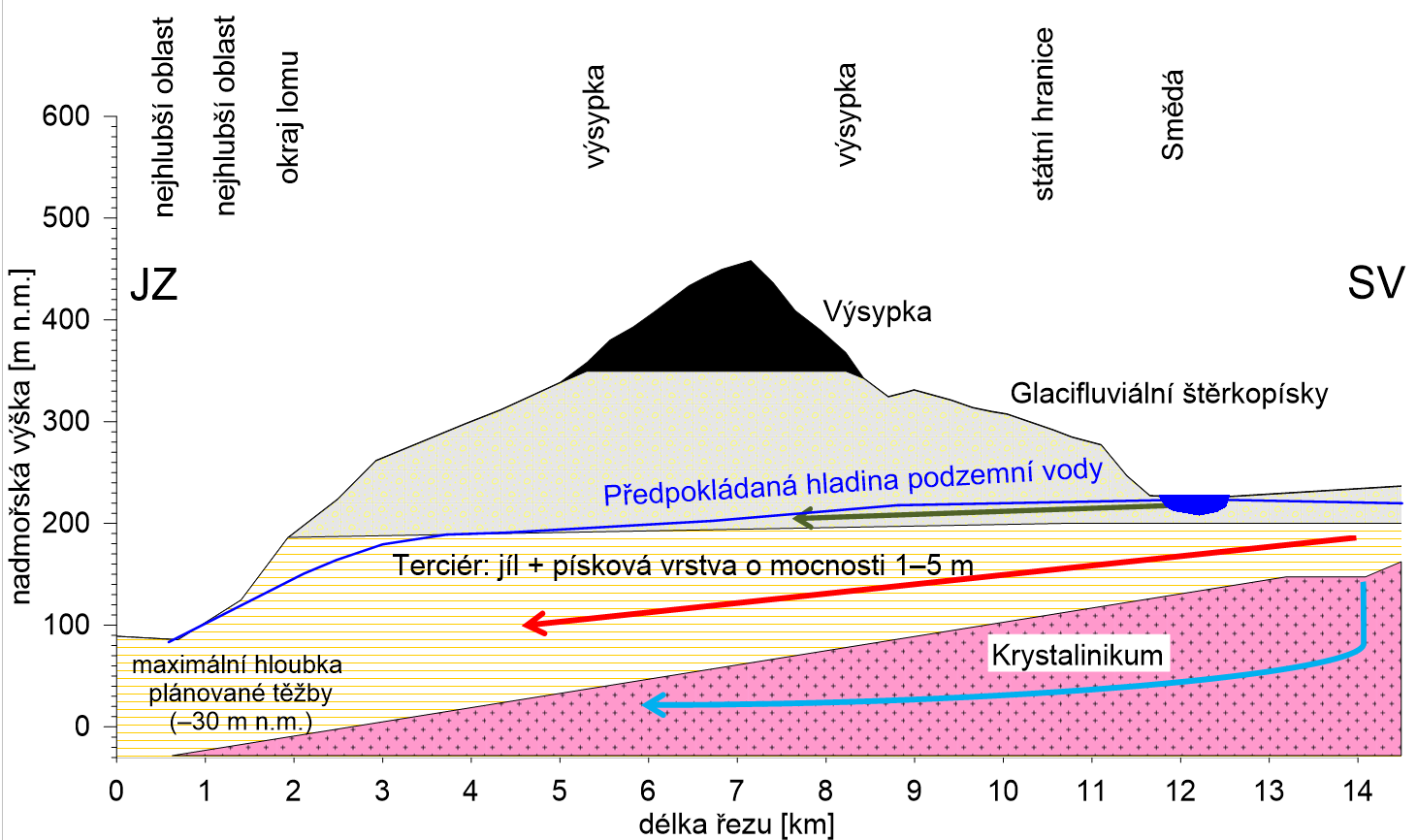 Obrázek 11: Ideový řez zájmovým územím – koncepční model
Obrázek 11: Ideový řez zájmovým územím – koncepční model
Tři hypotézy uvažují ovlivnění činností dolu Turów a jedna uvažuje pouze přirozené příčiny. Přirozenou možností, kam se může voda ztrácet, je subglaciální koryto (Králík 1989) – obrázek 12. Tato hypotéza není schopna vysvětlit pokles hladin podzemní vody, částečně však vysvětluje ztráty průtoku ve Smědé. Při přirozeném gradientu Smědé proudí podzemní voda nivou paralelně s tokem. Subglaciální koryto má možná podstatně větší transmisivitu než holocénní štěrkopísky na jih od Višňové. Je totiž cca 50 m hluboké, zatímco holocénní štěrkopísky v údolní terase jsou pouze cca 5 m mocné. Ztráty povrchové vody tak dotují poříční vodu v údolní nivě. Pokud by korytem měla proudit celá ztráta ze Smědé (240 l/s), bylo by třeba, aby hydraulická vodivost výplně glacifluviálního koryta byla 3∙10-3 m/s. To je hodnota velmi vysoká, proto ne příliš pravděpodobná, avšak rozhodně nikoli nemožná. Hypotéza ztráty vodnosti Smědé pouze v důsledku přetoku do subglaciálního koryta tedy nebyla vyvrácena.
Na J a Z od Filipovky se nachází podle hydrogeologické mapy 1:50 000 akumulace glacifluviálních sedimentů. Jejich báze není známa. Vzhledem k jejich možné propustnosti lze uvažovat, že přes ně dochází k proudění podzemní vody do dolu Turów. Pro tuto hypotézu však nemáme žádný přímý důkaz. Odtok vody z toku do dolu byl vypočten jako součin gradientu, šířky průtočného profilu a transmisivity. Z výpočtu vyplývá, že hydraulický spád mezi Smědou a dolem Turów je dostatečný, aby za předpokladu neověřených hydrogeologických podmínek způsobil prokázané ztráty průtoku ve Smědé. Hypotéza ztráty vodnosti pouze v důsledku přetoku přes glacifluviální sedimenty tedy nebyla vyvrácena.
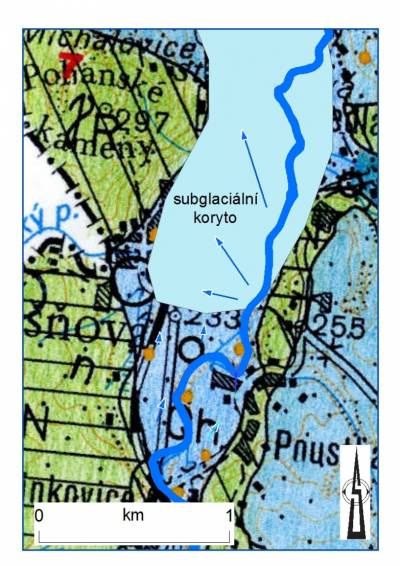 Obrázek 12: Hypotéza ztráty vodnosti v důsledku přetoku do subglaciálního koryta
Obrázek 12: Hypotéza ztráty vodnosti v důsledku přetoku do subglaciálního koryta
K přetoku podzemní vody do dolu Turów může také docházet přes písčité polohy v terciérních sedimentech. Polohy písku a štěrku o mocnosti 1–5 m byly zastiženy ve vrtech u Višňové (VA108, Viš23, Viš42), které však leží v mezipovodí I (mezi stanicemi Předlánce a Ostrožno), v němž až na výjimky ke zjevným ztrátám průtoku nedochází. Písčité polohy mohou být i v povodí II, ale archivní vrty zaznamenaly až do cca 60 m v terciéru pouze jíly. Nejvýznamnější pokles hladiny podzemní vody je pozorován ve vrtu VP2008 ve Višňové (mezipovodí I). Ač došlo k poklesu hladiny ve Višňové, byl zachován směr proudění (hydraulický gradient) z Polska do ČR. Výpočet kvantifikuje snížení přítoku z Polska do ČR v důsledku poklesu hladiny podzemní vody. Snížení přítoku vody z Polska (∆Q) byl vypočten jako součin rozdílu současného a původního gradientu (∆i), šířky průtočného profilu (Š) a transmisivity (T): ∆Q = ∆i ∙ Š ∙T. V důsledku poklesu hladiny ve vrtu o cca 40 cm došlo ke snížení přítoku podzemní vody do ČR ve Višňové nejvýše o 10 l/s. Takové množství se neprojeví výrazně na průtoku Smědé. Hypotéza ztráty vodnosti pouze v důsledku přetoku přes písčité vložky v terciérních sedimentech tedy byla vyvrácena.
K přetoku může taktéž docházet přes tektonické poruchy. Ztráty vody vlivem poruch by vysvětlovaly, proč k poklesu hladiny podzemní vody dochází na relativně rozsáhlém území a pokles není větší. Tato hypotéza nebyla pro neexistenci relevantních dat vůbec testována matematickým modelem. Hypotéza přetoku přes diskontinuity tedy nebyla testována a tedy ani vyvrácena.
Problematika ovlivnění Smědé dolem Turów je velmi obtížná a dále je ztížena nedostatkem relevantních dat. Ve skutečnosti se na ztrátách průtoku Smědé pravděpodobně podílejí všechna uvedená vysvětlení. Matematické modely umožnily maximálně vytěžit existující data a testovat hypotézy o příčině ztrát vodnosti Smědé. Jedna hypotéza byla vyvrácena. U jedné hypotézy byla vypočtena mezní hodnota hydraulické vodivosti pro vyvrácení hypotézy.
Srovnání jednoduchého a komplexního modelu – ovlivnění podzemních vod jezem
Kvantitativní hodnocení transportu kontaminantů z náplavů Labe při vybudování jezu u Děčína bylo prováděno ve dvou etapách pomocí analytického modelu (Nešetřil 2008c) a 2D vertikálního numerického modelu (Nešetřil 2009a). Jedná se tedy o srovnání jednoduchého a komplexního modelu.
Zájmové území je tvořeno fluviálními sedimenty Labe a podložními, zejm. křídovými horninami (obrázek 13), ze kterých přitéká do kvartéru značné množství vody – cca 45 l/s/km2. Cílem prací bylo vymezit možné transportní cesty kontaminantů při napouštění jezu i při jeho provozu a kvantifikovat potenciální ovlivnění kvality podzemní vody. Studie se zabývá šířením kontaminantů obsažených v náplavech Labe, které budou zatopeny v důsledku vzdutí jezu.
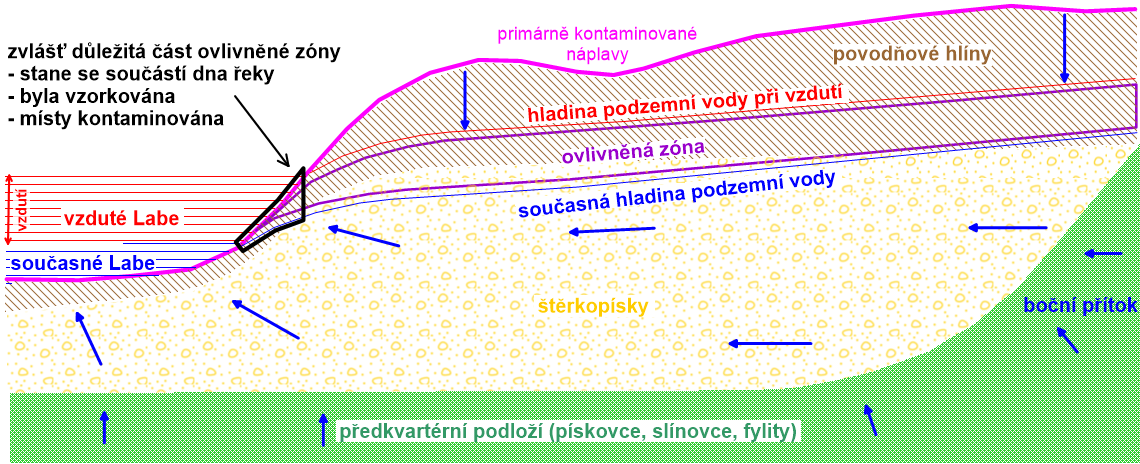 Obrázek 13: Schematický hydrogeologický řez a koncepční model
Obrázek 13: Schematický hydrogeologický řez a koncepční model
Byl sestaven matematický model (obrázek 14) transportu kontaminantů při
- napouštění jezu (kontaminanty pronikají do štěrkopískového kolektoru) a při
- návratu kontaminantů do Labe.
Jedná se tedy o transportní cesty při napouštění jezu a částečně při jeho provozu. Matematický model je odvozen z rovnice kontinuity. Nepočítá s Darcyho zákonem (neuvažuje hydraulickou vodivost). Uvažujeme tak nepříznivou variantu. Hydraulická vodivost štěrkopískového kolektoru je tak vysoká (až 9∙10-3 m/s), že při zatápění jezu (min. 1 měsíc) je dost času na ustálení proudění. Modelové řešení průniku kontaminantů do fluviálních sedimentů při zatápění jezu je odvozeno z úvahy, že objem kontaminované vody, která vnikne do kolektoru, je roven objemu suchých pórů, které jsou při zatápění zaplaveny. Takže platí:
L = š∙∆h/(M+∆h)
kde L je délka transportu [m], ∆h je vzdutí [m], š je dosah vzdutí v kolektoru [m] a M je původní mocnost zvodně [m]. Dosah vzdutí v kolektoru odpovídá šířce štěrkopískového kolektoru (nivy). V některých úsecích je šířka nivy značná (až cca 450 m). Protože dochází k přítokům z křídy na bocích štěrkopískového kolektoru, byl maximální dosah stanoven na základě hydrogeologického průzkumu v Děčíně-Rozbělesích (Skořepa 1993) na 450 m. Jedná se o vzdálenost od řeky, ve které se současná hladina podzemní vody rovná jezem vzduté hladině v Labi. Modelové řešení následného vytláčení kontaminantů v důsledku přirozených přítoků do fluviálních sedimentů počítá s tím, že těleso kontaminované vody je zatlačováno do Labe přítokem z boků (svahů), infiltrací a přítokem z křídy do části kolektoru, který není kontaminován. Samostatně byla vypočítána doba návratu v důsledku infiltrace a v důsledku bočních přítoků. Vzorec pro dobu návratu z důvodu infiltrace srážkových vod byl odvozen pomocí integrace, protože délka kolektoru nezasaženého kontaminací se v průběhu výpočtu mění. Pro dílčí doby návratu platí:
tr = (M+∆h)/r ∙ ln(š/(š-L)) ∙ n
kde
tr doba návratu v důsledku infiltrace srážkových vod [s]
r infiltrace [m/s]
n pórovitost [–] a
tq = L∙(M+∆h)/q∙n
tq doba návratu v důsledku bočních přítoků [s]
Celková doba návratu t [s] byla vypočtena podobně jako odpor dvou paralelně zapojených rezistorů.
t = tr∙tq /(tr+tq)
Zpomalení šíření kontaminantů ve štěrkopískovém kolektoru vlivem sorpce (retardace) byla zanedbána (nepříznivá varianta). Model předpokládá, že dno řeky je kontaminováno stejně jako vzorkované náplavy (nepříznivá varianta). Není uvažováno míšení vod v kolektoru. Modelové řešení bylo provedeno v tabulkovém kalkulátoru MS Excel.
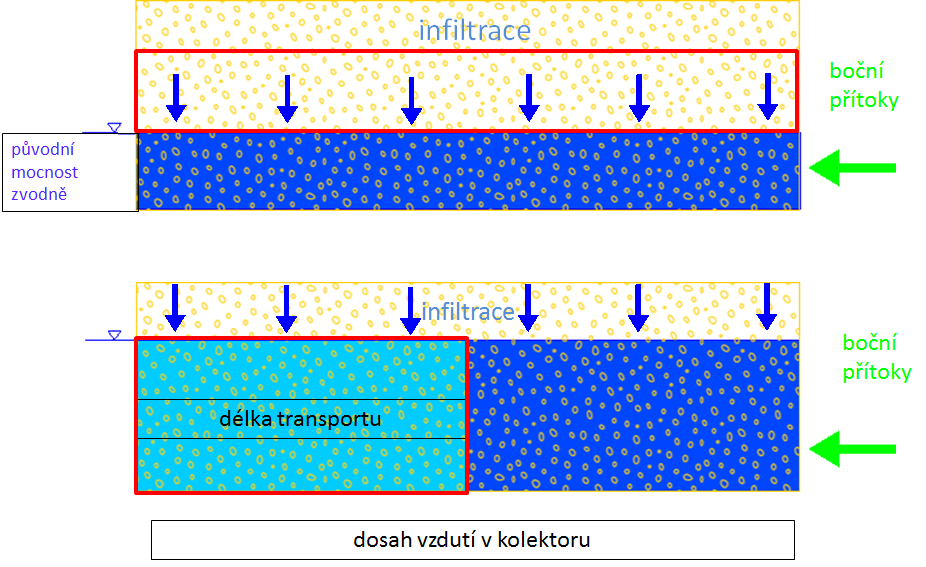 Obrázek 14: Schéma bilančního výpočtu: Objem pístu vody z řeky odpovídá zvětšení zvodně
Obrázek 14: Schéma bilančního výpočtu: Objem pístu vody z řeky odpovídá zvětšení zvodně
Výsledky modelu ukazují, že v extrémním případě by se kontaminace dostala cca 60 m od břehu, byla by však do cca devadesáti dní od začátku zvyšování hladiny v daném místě zatlačena zpět. Skutečnost bude však příznivější, protože model neuvažuje kolmataci dna, hydraulickou vodivost štěrkopísků, sorpci kontaminantů v štěrkopískovém kolektoru, kinetická omezení desorpce z náplavů ani hydrodynamickou disperzi a míšení vod v kolektoru. Studie prokázala, že vybudování jezu nebude mít dlouhodobý vliv na kvalitu podzemní ani povrchové vody.
Tato případová studie je jediná, která se zabývá rozsáhlým územím, které je z hydraulického hlediska velmi dobře prozkoumané. Nicméně znalosti o kontaminaci náplavů a jejich mobilitě nejsou dostatečné pro to, aby bylo opodstatněné využití komplexnějšího modelu. Již jednoduchý model prokázal, že vybudování jezu nebude mít dlouhodobý vliv na kvalitu podzemní ani povrchové vody a tak by komplexnější model nebyl lepším podkladem pro rozhodování.
Na základě požadavku oponenta bylo v další etapě (Nešetřil 2009a) navázáno na tento jednoduchý model sadou 2D vertikálních modelů (obrázek 15) provedených v MODFLOW a MT3D-MS. Byla tak vytvořena predikce relativních koncentrací ve 2D řezech, která však nepřispěla k lepšímu pochopení procesů. Výsledky nebyly podpořeny adekvátními daty. V důsledku vysoké hydraulické vodivosti nemá její konkrétní hodnota v modelu praktický význam, protože k průniku povrchové vody dochází téměř okamžitě. Do numerického modelu bylo třeba zadat storativitu a efektivní porozitu, které nejsou známy. V analytickém modelu však stačí zadat jejich poměr. Protože zjednodušeně jsou si tyto dvě veličiny pro zvodeň s volnou hladinou rovny, došlo k jejich vykrácení, a do analytického modelu se vůbec nezadávají.
Případová studie uplatňuje první bod návodu – Guidelines for effective modelling (Hill a Tiedeman 2007, s. 268) – „Start simple and add complexity…“
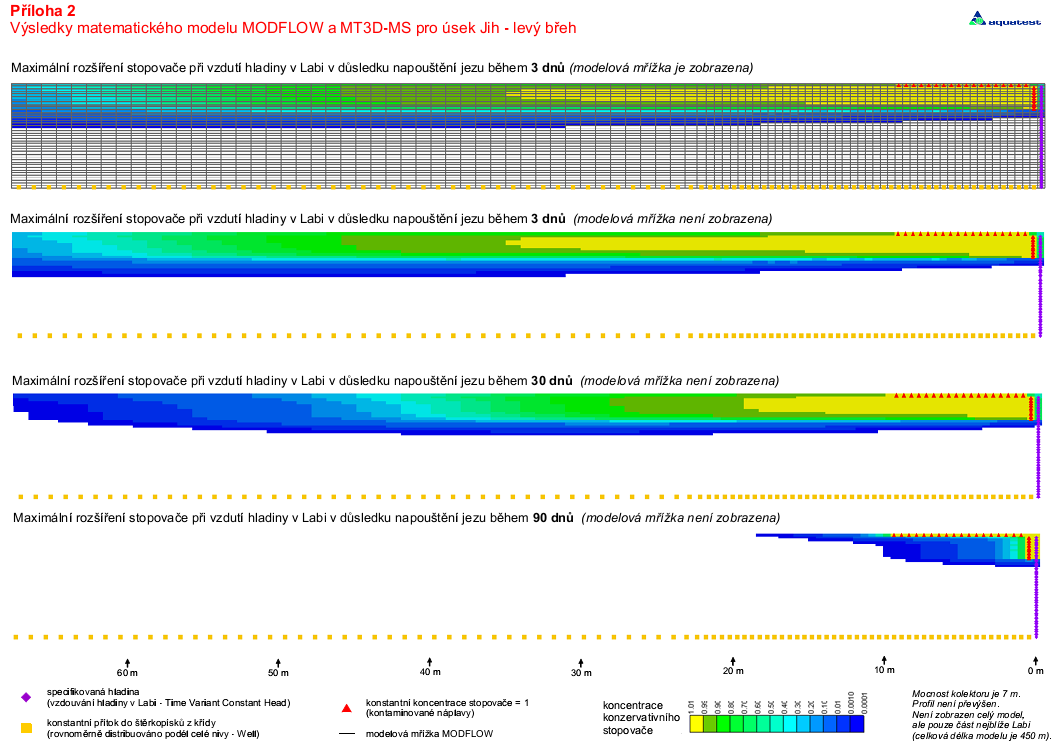 Obrázek 15: Numerický 2D vertikální model
Obrázek 15: Numerický 2D vertikální model
V následujících případových studiích se nemusí nutně uplatňovat ekvifinalita, ale vhodně volená kombinace jednoduchých modelů (přístupů) pro dosažení zvoleného cíle.
Kombinace principiálně odlišných modelů – model délky kontaminačního mraku a dovoleného čerpání
Modelová studie (Nešetřil 2008a) byla zpracována pro analýzu rizik staré ekologické zátěže ropnými uhlovodíky (RU) v areálu bývalého vojenského výcvikového prostoru. Bylo vypočítáno a hodnoceno:
- maximální rozsah oblasti zastižené v budoucnu kontaminací (na základě délky ustáleného kontaminačního mraku RU vypočítané pomocí modelu CoronaScreen) a
- dovolené čerpání v obci, které nebude přitahovat kontaminaci z potenciálně kontaminované oblasti.
Geologicky je území součástí české křídové pánve. Jsou zde dva kolektory – svrchní turonský a spodní cenomanský. Šíření kontaminace je myslitelné pouze v turonském kolektoru (déle jen „kolektor“) a to zejména v jeho svrchní části, která je přípovrchově rozpukaná, a proto propustnější.
Model ustálené délky kontaminačního mraku
Obecně lze říci, že se růst kontaminačního mraku vlivem biodegradace zpomalí. Po jisté době se již délka kontaminačního mraku nezvětšuje. Dojde totiž k dostatečnému promíšení vod a všechny transportované RU jsou postupně spotřebovávány biodegradačními reakcemi. Látkový tok RU z ohniska se tak rovná množství RU spotřebovaných biodegradačními reakcemi. Toto stádium se nazývá ustálený kontaminační mrak (steady state plume). Délka ustáleného kontaminačního mraku byla vypočítána pomocí programu CoronaScreen (Wilson et al. 2005). Je to soubor tří matematických modelů vyvinutých v rámci evropského projektu CORONA, na kterém se autor předkládané práce podílel. Výsledkem každého modelu je odhad délky ustáleného kontaminačního mraku. CoronaScreen počítá též čas nutný k dosažení ustáleného mraku. K tomu je třeba zadat rychlost šíření rozpuštěné látky, která se nesorbuje.
CoronaScreen obsahuje následující modely:
- Model bilance elektronů
- Analytický model
- Pohyblivý (travelling) 1D numerický model – využívá PHREEQC (Parkhurst a Appelo 1999)
CoronaScreen je screeningový model, který je na rozdíl od starších screeningových modelů – např. BIOSCREEN (Newell et al. 1997), BioScreen-AT (Karanovic a Neville 2014) či NAS (Widdowson et al. 2008) – zaměřen spíše na klíčové procesy ovlivňující přirozenou atenuaci než na distribuci koncentrací polutantů. CoronaScreen používá předpoklad, že ohnisko kontaminace má konstantní koncentraci a konstantní mocnost a že vstupní parametry jsou distribuovány uniformně. Na rozdíl od univerzálních numerických 3D transportních modelů – např. RT3D (Clement 1997) či MT3D-MS (Zheng 1998) – probíhá výpočet velmi rychle. Rychlost biodegradace je do značné míry určena mírou promíšení kontaminované vody a čisté vody obsahující elektronové akceptory. K míšení dochází především v reaktivní zóně na okraji mraku. Aby bylo možno modelovat šíření RU včetně biodegradace pro celou lokalitu, musí být mřížka transportního modelu dostatečně jemná, aby nedocházelo k nadhodnocení míšení kontaminované a nekontaminované vody. Nadhodnocení míšení způsobuje nadhodnocení rozkladu RU (biodegradace). CoronaScreen tento nedostatek nemá. CoronaScreen je speciální model určený pro modelování přirozené atenuace, a ve srovnání s univerzálními numerickými transportními modely je proto v mnohém účelnější.
Vstupními daty modelů CoronaScreen jsou:
- hydrogeologické charakteristiky (rychlost proudění, pórovitost, koeficient retardace),
- transportní charakteristiky (disperzivity či mocnost reaktivní zóny),
- šířka a mocnost kontaminačního mraku,
- koncentrace kontaminantů a elektronových akceptorů v pozadí a v ohnisku.
Velkou výhodou CoronaScreen ve srovnání s univerzálními 3D simulátory (např. RT3D) je, že CoronaScreen:
- dobře pracuje s disperzí (dostatečná diskretizace, pokud je vůbec potřeba),
- používá více metod,
- byl vyvinut právě pro přirozenou atenuaci.
Model dovoleného čerpání
Na základě modelu bylo stanoveno, jaké množství podzemní vody je možno čerpat v obci. Čerpání nemá ovlivnit přirozený směr proudění podzemní vody v oblasti maximálního možného rozšíření kontaminace. Kontaminace se tak nebude šířit do nekontaminované oblasti na sever a směrem k využívaným studním v obci.
Dovolené čerpané množství Q bylo stanoveno tak, aby hydraulická deprese vyvolaná tímto čerpáním nedosáhla k oblasti maximálního možného rozšíření kontaminace. Hydraulickou depresí pro tento účel rozumíme oblast, pro kterou platí současně, že se zde:
- projevuje snížení hladiny podzemní vody vyvolané čerpáním Q z využívané studny,
- veškerá podzemní voda (z části kolektoru vertikálně zastiženého využívanou studnou) je vyčerpána využívanou studnou.
Vstupní data jsou uvedena v tabulce 8.
Tabulka 8: Vstupní data modelu dovoleného čerpání
| Parametr | Hodnota | Zdroj informací |
|---|---|---|
| Hydraulický gradient i | 0,2% (tj. 0,002) | Přibližně maximum přímých měření |
| Transmisivita T | 1∙10-5 m2/s | Součin zastižené mocnosti a hydraulické vodivosti: 10 m ∙ 1∙10-6 m/s |
| Infiltrace q | 0,5 l/s/km2 = 5∙10-10 m/s | Dolní mez odhadu zmenšena na polovinu z důvodu existence zastavěných ploch, kde srážková voda nemůže infiltrovat |
| Oblast maximálního možného rozšíření kontaminace | Polygon viz obrázek 16 | Oblast šíření kontaminace stanovená na základě možného směru proudění podzemní vody a délky ustáleného kontaminačního mraku |
| Vzdálenost k oblasti maximálního možného rozšíření kontaminace L | Specifická hodnota pro každou využívanou studnu [m] | Přímá vzdálenost mezi využívanou studnou, pro kterou je počítáno Q, a oblastí maximálního možného rozšíření kontaminace |
Dovolené čerpané množství Q je dáno součtem dílčích přítoků Q1 a Q2.
Přítok Q1 je přítok z oblasti mimo hydraulickou depresi, která byla vyvolána čerpáním Q.
Q1 = T∙i∙2L
Přítok Q2 je dán infiltrací srážkových vod do oblasti hydraulické deprese.
Q1 = π∙L2∙q,
a tedy Q = Q1+Q2. Za zadaných podmínek je Q1 ≪ Q2. Výsledky modelů jsou zobrazeny níže (obrázek 16).
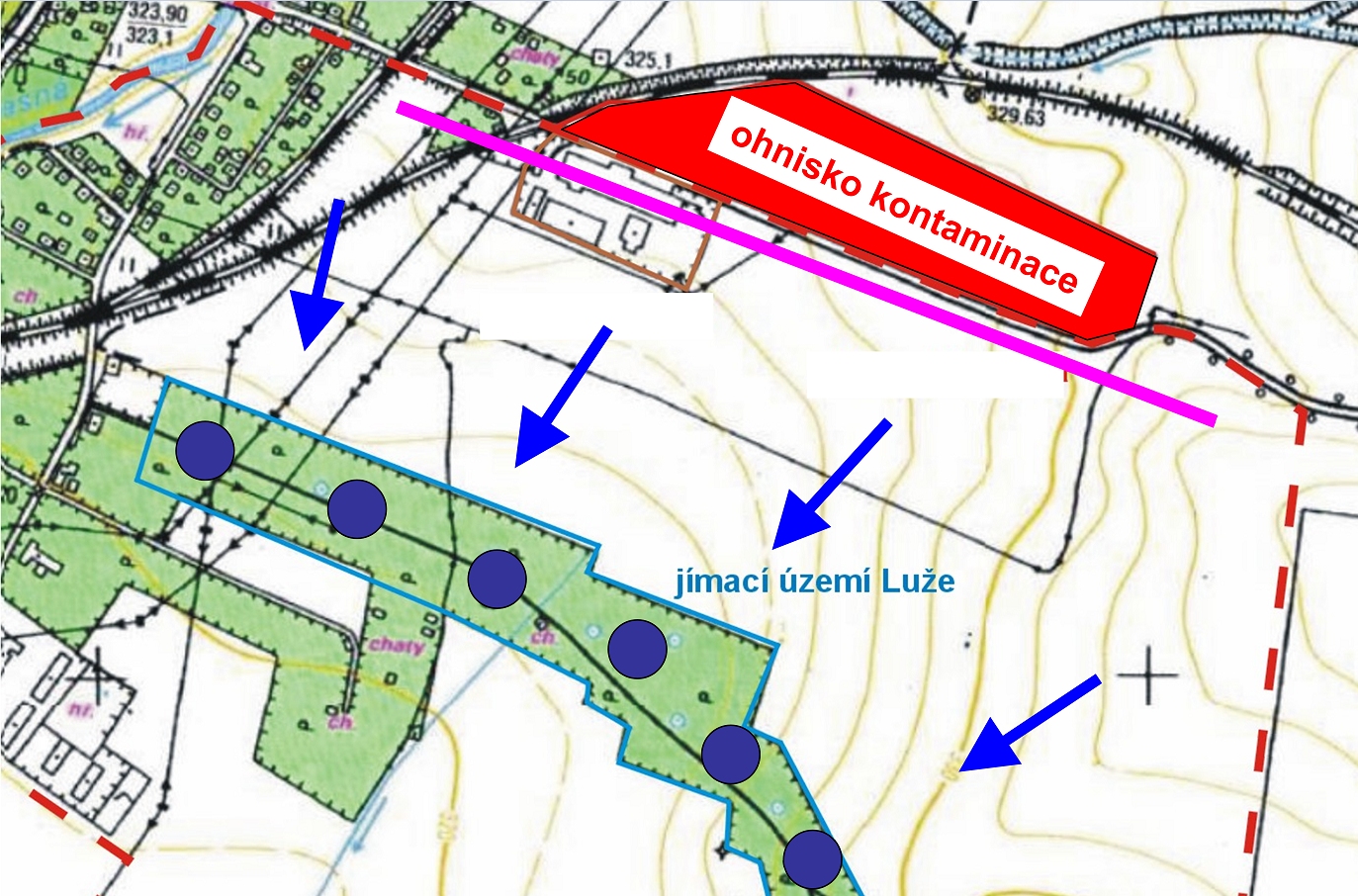
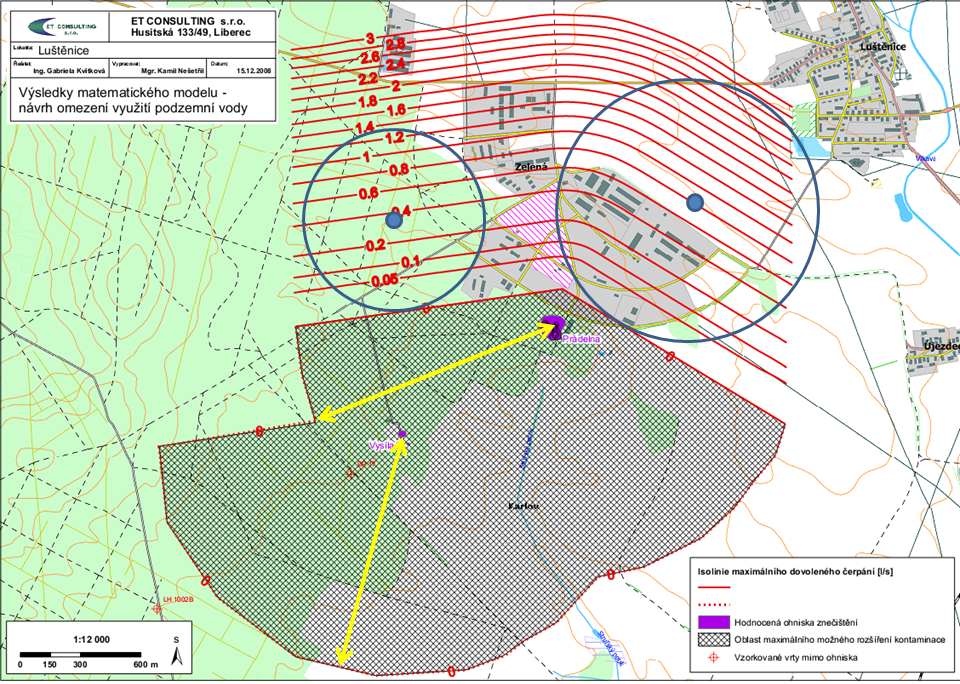 Obrázek 16: Výsledky modelu ustálené délky kontaminačního mraku (oblast max. možného rozšíření kontaminace) a modelu čerpání (isolinie). Žluté šipky představují maximální délku kontaminačního mraku. Kruhy mají poloměr L.
Obrázek 16: Výsledky modelu ustálené délky kontaminačního mraku (oblast max. možného rozšíření kontaminace) a modelu čerpání (isolinie). Žluté šipky představují maximální délku kontaminačního mraku. Kruhy mají poloměr L.
Pro specifický účel byla využita unikátní kombinace modelů, která dala praktický návrh na využívání podzemních vod v okolí kontaminovaného území. V případě modelu délky ustáleného kontaminačního mraku se uplatnil princip ekvifinality (tři metody výpočtu téhož). Ve standardním numerickém transportním modelu by docházelo k numerické disperzi, která by mohla vést k rychlejší biodegradaci kontaminantu – na druhou stranu by bylo možno zpomalovat odbourávání zahrnutím kinetiky. Model čerpání by bylo nutno realizovat jen pro explicitně zadané plánované studny. To by bylo možno automatizovat např. s využitím sady skriptů FloPy (Bakker et al. 2016), která umožňuje vytvářet a upravovat modely v MODFLOW a navazujících sw za pomoci programovacího jazyka Python.
Aktualizované analýze rizik (v rámci které vznikl prezentovaný model) předcházela analýza rizik. V rámci ní byl zpracován numerický model šíření kontaminace (MODFLOW, MT3D). Jeho využití pro předkládanou studii by nebylo účelné. Na tuto případovou studii by bylo možno navázat analytickým řešením tzv. „capture zone” – např. Zhou a Haitjema (2012).
Transport ropných uhlovodíků
Další případová studie demonstruje využití většího množství relativně jednoduchých (zejm. analytických) modelů pro hodnocení přirozené atenuace ropných uhlovodíků. Jsou využity modely založené na Darcyho zákoně, vodní bilanci, látkových tocích i aplikaci simulačního softwaru. Model je podrobně dokumentován ve zprávě (Nešetřil 2008b), jež je přílohou analýzy rizika (Kubricht 2008). Výsledky byly publikovány v konferenčním sborníku (Nešetřil 2009b).
Pro potřeby aktualizované analýzy rizik (stanovení sanačních limitů) bylo hodnoceno šíření RU a jejich přirozená atenuace. Ohnisko (obrázek 17) kontaminace RU se nachází v distribučním skladu pohonných hmot (DS). Podzemní voda proudí jv směrem k vodárenskému jímacímu území (JÚ) vzdálenému 400 m, které je používáno k zásobování obyvatelstva pitnou vodou.
Vstupní data
V rámci průzkumu pro analýzu rizik bylo provedeno 20 sond a vrtů, geofyzikální průzkum (geoelektrické, seismické a karotážní metody), analýzy kontaminantů v podzemní vodě a v zemině a indikátorů přirozené biodegradace ve vodě. Byly vymezeny koncentrace elektronových akceptorů a produktů biodegradace v pozadí, ohnisku kontaminace a v kontaminačním mraku.
Dále byla stanovena oxidační kapacita pevné fáze pomocí
- extrakčních metod – určení obsahu mikrobiálně přístupného Fe3+ a Mn4+ podle metodiky Herona et al. (1994a; 1994b) a
- elektronové mikroskopie (určení vzniku, kvantity a stechiometrického složení sekundárně vznikajících minerálů za pomoci rastrovacího elektronového mikroskopu (SEM) a rentgenové difraktometrie (XRD).
Oxidační kapacita v kontaminované části lokality byla výrazně nižší než v nekontaminované. Výsledky ukazují, že nejvyšší podíl elektronových akceptorů vhodných pro mikrobiální degradaci RU je vázán v oxidech a hydroxidech železa a že jsou využívány k biodegradaci RU. Stanovení oxidační kapacity pevné fáze není standardní metoda. Vzorky je třeba odebrat a přechovávat v dusíkové atmosféře a ihned zamrazit.
Na základě zkušeností z řešení obdobných úkolů se ukazuje, že jsou data, která jsou pro predikce velmi důležitá (tabulka 9). Je jimi zejména plošné měření fyzikálně-chemických parametrů (pH, Eh) a určení hlavních indikátorů přirozené biodegradace (rozpuštěný kyslík, dusičnany, sírany, amonné ionty, dusitany). Naopak plošné stanovování všech hlavních anorganických makrokomponent („úplný chemický rozbor“) se ukazuje jako málo účelné – pro případné termodynamické modelování by však bylo nezbytné.
Tabulka 9: Vstupní data pro hodnocení přirozené atenuace
| Důležitá | Málo důležitá | |
|---|---|---|
| Dostupná | pH, Eh, rozpuštěný kyslík, dusičnany, sírany, amonné ionty, dusitany, alkalita, koncentrace kontaminantů, ropné bakterie, hydraulický gradient, transmisivita, org. uhlík. v pevné fázi; historie zdrojů, šíření kontaminace a sanačních zásahů | plošné stanovování všech hlavních anorganických makrokomponent |
| Obtížně dostupná | oxidační kapacita pevné fáze vertikální rozsah mraku mocnost reaktivní zóny (či vertikální disperzivita) zóny prioritního proudění |
Úbytek elektronových akceptorů, nárůst produktů biodegradace, rozbory pevné fáze a mikrobiologické rozbory prokázaly, že přirozená biodegradace probíhá. Matematický model se pak pokusil tyto procesy kvantifikovat.
Matematický model
Doba transportu
Byla spočítána doba potřebná pro šíření (tj. doba transportu či doba doběhu kontaminantu) RU z DS do JÚ. Ta byla vypočítána na základě retardačního koeficientu (hydrofobní sorpce podle lineární isotermy) a rychlosti šíření konzervativního stopovače, jež byla vypočtena podle:
- Darcyho zákona (na základě hydraulického gradientu, hydraulické vodivosti a pórovitosti) a
- bilančního výpočtu (na základě úvahy, že konzervativní stopovač se dostane do JÚ za dobu, kdy je vyčerpán objem vody mezi DS a JÚ).
Výsledky uvedených modelů byly pozoruhodně blízké – rozdíl odpovídal cca 13 %.
Látkové toky
Látkovými toky RU je myšleno množství RU, které proteče kontrolním profilem za jednotku času (např. kolik kg/rok RU vyteče z ohniska, přes linii monitorovacích vrtů či přiteče do recipientu). Byl spočítán:
- látkový tok RU přes linii monitorovacích vrtů (součin koncentrace RU v jednotlivých vrtech, transmisivity kontaminované zvodně, hydraulického gradientu a délky kontrolního profilu),
- látkový tok RU do JÚ (součin čerpaného množství a průměrné koncentrace RU v čerpaných vrtech nebo ve sběrném potrubí před úpravou),
- inverzní úloha (jaká je bezpečná koncentrace RU v linii monitorovacích vrtů na okraji DS tak, aby byly v JÚ dosaženy limity upravitelnosti vody). Inverzní úloha vychází z porovnání látkového toku přes linii monitorovacích vrtů a toku do JÚ.
Látkový tok RU do JÚ se v průběhu času víceméně snižuje. Látkový tok z DS byl vždy větší než tok do JÚ. To je indikátorem probíhající přirozené atenuace. Avšak výpočet doby transportu ani látkových toků biodegradaci přímo nezahrnují.
Bilance biodegradace
Na základě koncentrací elektronových akceptorů a produktů biodegradace v pozadí a v DS byl vypočítán úbytek elektronových akceptorů při průtoku vody ohniskem. Z úbytku bylo pomocí tzv. „BTEX utilization factor“ vypočítáno množství RU, které jsou biodegradovány přímo v ohnisku.
Model ustálené délky kontaminačního mraku
Pomocí modelů CoronaScreen (kapitola výše) byla vypočítána délka ustáleného kontaminačního mraku. Byly vypočítány maximální koncentrace v JÚ při současném stavu kontaminace v DS. Byly vypočítány koncentrace v DS tak, aby ustálený kontaminační mrak dosahoval právě k JÚ, které tak nebude ohroženo.
Výsledky modelu jsou citlivé na mocnost reaktivní zóny, již je možno zjistit z vrtů osazených víceúrovňovými vzorkovači. Na předmětné lokalitě byla mocnost reaktivní zóny vypočítána na základě vertikální disperzivity z literatury. Oxidační kapacita pevné fáze naopak tak důležitým vstupem není. Oxidační kapacita pevné fáze se uplatní obzvláště, pokud je hodnoceno šíření RU do nekontaminovaného kolektoru před dosažením ustáleného kontaminačního mraku včetně doby tohoto ustalování.
Tabulka 10: Shrnutí případové studie „Transport ropných uhlovodíků“
| Výsledek | Způsob výpočtu |
|---|---|
| Doba transportu | Darcyho zákon |
| Bilanční výpočet (konzervativní stopovač se dostane do JÚ za dobu, kdy je vyčerpán objem vody mezi zdrojem a jímacím územím) | |
| Látkové toky kontaminantů | Ze zdroje vs. vyčerpáno vodárenskými vrty |
| Zpětná úloha (jaká je bezpečná koncentrace kontaminace ve zdroji tak, aby v jímacím území byly dosaženy limity) | |
| Bilance biodegradace Množství odbouraného kontaminantu | Pokles elektronových akceptorů při průtoku ohniskem |
| Ustálená délka kontaminačního mraku (Koncentrace v ohnisku, aby kontaminační mrak nedosáhl do jímacího území) | Model bilance elektronů (CoronaScreen) |
| Analytický model (CoronaScreen) | |
| Pohyblivý 1D numerický model (CoronaScreen) |
Byly provedeny modelové výpočty od jednoduchých analytických modelů až k použití screeningového modelu CoronaScreen. Modely vycházely z různých předpokladů. Výsledky modelů pro dobu transportu byly pozoruhodně blízké – rozdíl odpovídal cca 13 %. Délka ustáleného kontaminačního mraku vypočítaná analytickým modelem byla 2× až 3× větší než pomocí bilance elektronů. Využité modely dávají konkrétní odpovědi (kdy, kolik, jestli vůbec, účinnost biodegradace) a naznačují nejistotu výsledků. Využití různých typů modelů umožnilo využití a vytěžení všech typů dostupných dat.
Transport chlorovaných uhlovodíků – advekční a bilanční model
Na lokalitě byla řešena (Nešetřil 2012) problematika transportu chlorovaných uhlovodíků do studní pro individuální zásobení podzemní vodou a do vodárenských vrtů. Ohnisko kontaminace je v málo propustném kvartérním kolektoru (hydraulická vodivost 10-6 m/s), ale k čerpání ve vodárenských vrtech HV1 a L2 (obrázek 18) dochází v propustném cenomanském kolektoru (hydraulická vodivost 10‑4 m/s). Přirozeně byly hladiny v jednotlivých kolektorech na srovnatelné úrovni, ale v důsledku čerpání je nyní hladina v cenomanu níže.
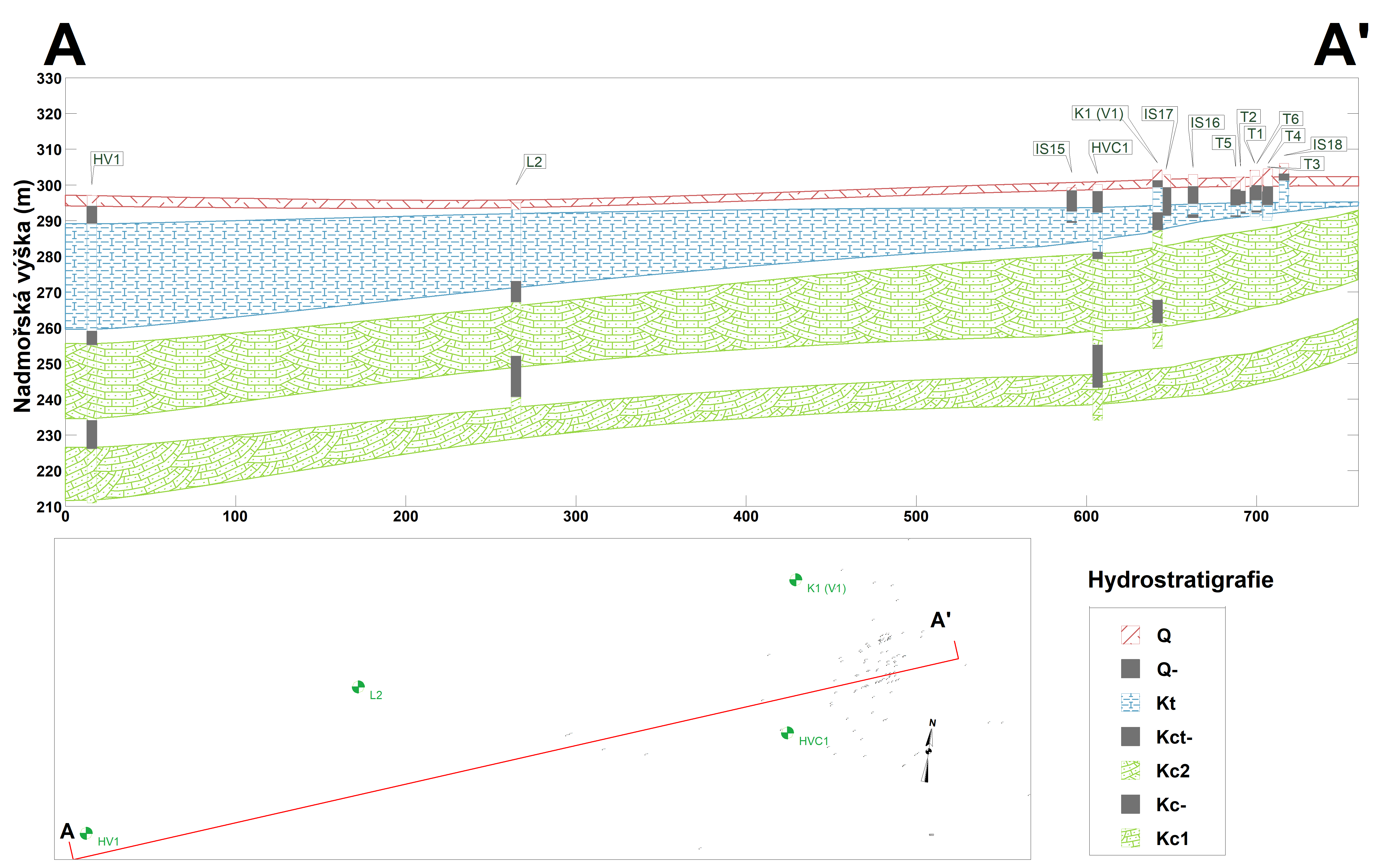 Obrázek 18: Hydrostratigrafický řez s vyznačením kvartérního (Q), turonského (Kt) a dvou cenomanských kolektorů (Kc1, Kc2) – šipky naznačují koncept bilančního modelu
Obrázek 18: Hydrostratigrafický řez s vyznačením kvartérního (Q), turonského (Kt) a dvou cenomanských kolektorů (Kc1, Kc2) – šipky naznačují koncept bilančního modelu
Advekční model – predikce
Na lokalitě jsou dva čerpané vrty L2 a HV1, které se po dvou týdnech střídají v čerpání 13 l/s. První způsob spočíval ve výpočtu doby, za kterou by se mohla kontaminace dostat kvartérním kolektorem ke studnám individuálního zásobování a cenomanským kolektorem k bližšímu (L2) ze dvou jímacích vrtů (L2 a HV1). Advekční model je založen na Darcyho zákonu a na rovnici kontinuity.
Proudění v cenomanském kolektoru je určeno především čerpáním ve vodárenských vrtech (radiální proudění) a je proto nutno uvažovat 2D proudění. Model je založen na metodě analytických elementů (AEM), je implementován s pomocí grafického uživatelského rozhraní Visual AEM (Craig a Matott 2009) a byl implementován v simulačním kódu Bluebird / Cardinal. Byly vypočítány hydroizopiezy cenomanské zvodně a particle tracking.
Výsledkem obou advekčních modelů je odhad doby doběhu kontaminace. Nejkratší doběhové doby vycházejí u cenomanského kolektoru. Koncentracemi ClU v jímacích vrtech v důsledku šíření v cenomanské zvodni se proto zabývá navazující bilanční model.
Bilanční model – testování hypotézy
Druhý přístup kvantifikuje přetok podzemí vody a kontaminace mezi kolektory. Bylo vypočítáno, jaká koncentrace ClU v jímacím vrtu odpovídá tomuto toku ClU.
Byl vypočítán hmotnostní tok ClU do cenomanské zvodně na základě rozdílů hladin v jednotlivých zvodních, mocnosti a propustnosti izolátorů a plochy kontaminované zvodně o dané koncentraci ClU. Byly vypočítány alternativy toku přímo z kvartérní zvodně a z turonské zvodně. Bylo uvažováno, že veškeré ClU, které přetečou do cenomanské zvodně, budou rovnoměrně naředěny ve vodě čerpané z vodárenského vrtu. Tak byla vypočítána koncentrace ClU ve vodárenském vrtu L2 – 0,032 μg/l odpovídá látkovým tokům ClU z kvartérního kolektoru a 0,025 μg/l tokům z turonu. Tyto hodnoty jsou neočekávaně nízké. Jsou výrazně menší než měřené koncentrace ve vodárenském vrtu L2 (0,83 μg/l TCE a 0,55 μg/l PCE). Když se obdobný výpočet provede pro koncentrace ClU v turonské zvodni před začátkem sanace, vyjdou koncentrace ClU ve vodárenském vrtu L2 přibližně 12krát větší (0,30 μg/l), což je však stále výrazně méně než měřené koncentrace ClU. To naznačuje, že cenomanský kolektor byl pravděpodobně kontaminován ClU v důsledku gravitačního proudění volnou fází ClU (DNAPL). Zatímco rozpuštěné ClU migrující puklinou v izolátoru difundují do bloku horniny, tak DNAPL – podobně jako koloidy (např. nanočástice) – difúzi nepodléhají, a mohou migrovat mnohem snáze než konzervativní stopovač (Parker et al. 1994). Model uvažuje šíření rozpuštěných ClU advekcí, nikoliv fáze DNAPL ClU. Fáze se může svisle šířit i proti směru proudění podzemní vody. Šíření fáze je obtížně kvantifikovatelné a nejsou k němu pro tuto lokalitu dostupná data.
Vypočítané intenzity přetoku podzemní vody mezi kolektory jsou nerealisticky veliké. Ve výpočtu se totiž nejedná o bilancování vody pro celou lokalitu, ale o výpočet, který prokázal, že ani tak absurdně veliké toky nejsou schopny generovat měřené koncentrace ClU ve vodárenském vrtu L2. Úvaha ukazuje na to, že kontaminace se vertikálně šířila především jako DNAPL. Jedná se myšlenkový experiment, kterým testujeme hypotézu, zda jsou měřené koncentrace rozpuštěných ClU schopny ovlivnit kvalitu vody ve vodárenských vrtech. Jedná se o nejpesimističtější myslitelný scénář.
Bylo by možno sestavit distribuovaný numerický model. Aby byl takový model smysluplný, bylo by třeba shromáždit a interpretovat data z širšího okolí ohniska kontaminace a jímacích vrtů. Celistvý analytický model umožňuje přímou interakci s uživatelem („ne-modelářem“) a snadné porozumění implementaci modelovaných procesů. Je transparentní a snadno reprodukovatelný. Není přeparametrizovaný, což znamená, že se do modelu nezadávají parametry, jež nejsou pro výpočet skutečně významné. Výhodou takového jednoduchého modelu je mj. možnost snadno zpracovávat variantní výpočty, které jsou uvedeny ve zprávě v příloze E na přiloženém CD (Nešetřil 2012).
Model vyvrátil implicitní hypotézu, že je rozhodující transport rozpuštěných ClU. Složitější model by pouze zamlžil vztah mezi předpoklady a důsledky. Vyskytovaly by se v něm totiž další veličiny a procesy (např. čas, disperzivita).
Hodnocení nejistoty koncepčního modelu podle Refsgaarda et al. 2006
Nejistota koncepčního modelu předložených případových studií byla posouzena podle metodiky (Refsgaard et al. 2006). Všechny případové studie je možno charakterizovat následně (tabulka 11):
Tabulka 11: Matice rodokmenu (pedigree) podle Refsgaarda et al. (2006) pro prezentované případové studie
| Skóre | Podložení empirickými důkazy | Teoretické porozumění | Reprezentace porozumění procesům | Věrohodnost | Shoda názorů odborníků | |
|---|---|---|---|---|---|---|
| Reprezentativnost | Kvalita a kvantita | |||||
| 15 | Bez přímé vazby (0) | Archivní/terénní data, neřízené experimenty, malé vzorky, přímá měření (3) | Prověřená teorie (4) | Jednoduchý model s agregovanými parametry (2) | Vysoce věrohodný (4) | Konkurenční školy (2) |
Modely vycházejí z archivních dat, která jsou většinou doplněna terénními měřeními. Nejsou dostupné dlouhodobé časové řady. Nejsou dostupná data pro kalibraci modelu ani jeho verifikaci. Model je postaven na prověřených teoriích, jež jsou v modelu implementovány v zjednodušené formě. Jednoduchost modelu umožňuje jeho pochopení a posouzení hydrogeology „ne-modeláři“. Nemusí však existovat shoda mezi odborníky, zda dostupná data jsou dostatečná a zda zjednodušení modelu není příliš veliké. Všechny možnosti hodnot z tabulky 11 uvádí tabulka 5.
Srovnání případových studií
Případové studie jsou srovnány v následujících tabulkách 12 a 13. Je zde uvedeno, čím se liší.
Tabulka 12: Stručné srovnání případových studií
| Různé … | Lokalita: | Smědá | Jez | Luštěnice | Vikýř. | Hořice |
|---|---|---|---|---|---|---|
| Typ dat | ||||||
| Procesy | ✔ | |||||
| Doména | část území, hloubka | ✔ | ✖ | ✔ | ✖ | ✔ |
| Aparát | analytické, anal. elementy, numerické | ✖ | ✔ | ✖ | ✔ | |
| Prostor. rozlišení | celistvý, distribuovaný | ✖ | ✔ | ✔ | ||
| Výsledná veličina | rychlost, bilance | ✖ | ✔ | ✔ |
Tabulka 13: Podrobné srovnání případových studií
| Různé … | Lokalita: | Smědá | Jez | Luštěnice | Vikýř. | Hořice |
|---|---|---|---|---|---|---|
| Typ dat | ||||||
| Procesy | ✔ | |||||
| Doména | část území | ✔ | ✔ | ✖ | ✔ | |
| hloubka | ✔ | ✖ | ✖ | ✖ | ✔ | |
| Aparátu | analytické | ✔ | ✔ | ✔ | ✔ | ✔ |
| anal. elementy | ✖ | ✖ | ✖ | ✖ | ✔ | |
| numerické | ✖ | ✔ | ✔*† | ✔* | ✖ | |
| Prostor. rozlišení | celistvý | ✔ | ✔ | ✔ | ✔ | ✔ |
| distribuovaný | ✔ | ✔ ČERPÁNÍ | ✖ | ✔ AE | ||
| Výsledná veličina | rychlost/doba | ✖ | ✔ | (✔) | ✔ | ✔ |
| bilance | ✔ | ? | ✔ | ✔ | ✔ |
*) PHREEQC v rámci CoronaScreen
°) PHREEQC samostatně
†) numerické distribuované modely MODLFLOW a MT3D byly využity v předcházející AR
Použitá literatura
BAKKER, M., V. POST, C. D. LANGEVIN, J. D. HUGHES, J. T. WHITE, J. J. STARN a M. N. FIENEN, 2016. Scripting MODFLOW model development using Python and FloPy. Groundwater. ISSN 1745-6584. DOI: 10.1111/gwat.12413
CLEMENT, T. Prabhakar, 1997. RT3D : A modular computer code for simulating reactive multi-species transport in 3-dimensional groundwater systems. Richland, WA, USA: Pacific Northwest National Laboratory. https://www.pnnl.gov/features-rt3d
CRAIG, James R. a L. Shawn MATOTT, 2009. Visual AEM. Waterloo, Canada: University of Waterloo. https://www.civil.uwaterloo.ca/jrcraig/visualaem/main.html
HERON, Gorm, Catherine CROUZET, Alain C. M. BOURG a Thomas H. CHRISTENSEN, 1994a. Speciation of Fe(II) and Fe(III) in contaminated aquifer sediments using chemical extraction techniques. Environmental Science & Technology. 28(9), 1698–1705. ISSN 0013-936X. DOI: 10.1021/es00058a023
HERON, Gorm, Thomas H. CHRISTENSEN a Jens C. TJELL, 1994b. Oxidation capacity of aquifer sediments. Environmental Science & Technology. 28(1), 153–158. ISSN 0013-936X. DOI: 10.1021/es00050a021
HILL, Mary C. a Claire R. TIEDEMAN, 2007. Effective groundwater model calibration : with analysis of data, sensitivities, predictions, and uncertainty. Hoboken N.J.: Wiley-Interscience. ISBN 978-0-471-77636-9.
KARANOVIC, M. a C. J. NEVILLE, 2014. BIOSCREEN-AT. USA: S.S. Papadopulos & Associates, Inc. https://www.sspa.com/software/bioscreen
KRÁLÍK, František, 1989. Nové poznatky o kontinentálních zaledněních severních Čech. Sborník geol. věd – Antropozoikum. (19), 9–74. ISSN 0036-5270.
KUBRICHT, Jiří, 2008. Distribuční sklad PHM společnosti Benzina a.s. Lokalita Šumperk-Vikýřovice : Analýza rizik starých ekologických zátěží. Závěrečná zpráva. České Budějovice: ENVIRO C.B. s.r.o.
NEŠETŘIL, Kamil, 2008a. Aktualizovaná analýza rizika na lokalitě Luštěnice : Matematický model. Závěrečná zpráva. Liberec: ET CONSULTING s.r.o.
NEŠETŘIL, Kamil, 2008b. DS PHM Benzina a.s. Šumperk-Vikýřovice Matematický model. Závěrečná zpráva. Praha: AQUATEST a.s.
NEŠETŘIL, Kamil, 2008c. Jez u Děčína : Šíření kontaminace z náplavů : Kvantitativní hodnocení. Závěrečná zpráva 253070498000. Praha: AQUATEST a.s.
NEŠETŘIL, Kamil, 2009a. Jez u Děčína : Šíření kontaminace z náplavů : Matematický model. Závěrečná zpráva 253090036000. Praha: AQUATEST a.s.
NEŠETŘIL, Kamil, 2009b. Modelování šíření a přirozené atenuace ropných uhlovodíků – praktická aplikace. In: Naďa RAPANTOVÁ a Arnošt GRMELA, ed. Voda – strategická surovina pro 21. století : Sborník 10. Česko-Slovenského mezinárodního hydrogeologického kongresu : 31. 8. – 3. 9. 2009. Ostrava: VŠB – Technická univerzita, Esmedia DTP s.r.o., s. 163–166. ISBN 978-80-248-2026-2.
NEŠETŘIL, Kamil, 2012. Matematický model podzemní vody: areál firmy KAR-BOX s.r.o. Hořice. Závěrečná zpráva. Liberec: Technická univerzita v Liberci.
NEWELL, Charles J., R. Kevin MCLEOD a James R. GONZALES, 1997. BIOSCREEN, Natural Attenuation Decision Support System. USA: US EPA.
PARKER, Beth L., Robert W. GILLHAM a John A. CHERRY, 1994. Diffusive disappearance of immiscible-phase organic liquids in fractured geologic media. Groundwater. 32(5), 805–820. ISSN 0017-467X. 10.1111/j.1745-6584.1994.tb00922.x
PARKHURST, David L. a C.A.J. APPELO, 1999. User’s guide to PHREEQC (version 2) — A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. Water-Resources Investigations Report 99-4259. Denver, Colorado: U.S. Department of the Interior, U.S. Geological Survey.
REFSGAARD, Jens Christian, Jeroen P. VAN DER SLUIJS, James BROWN a Peter VAN DER KEUR, 2006. A framework for dealing with uncertainty due to model structure error. Advances in Water Resources. 29(11), 1586–1597. ISSN 0309-1708. DOI: 10.1016/j.advwatres.2005.11.013
SKOŘEPA, Jaroslav, 1993. Děčín Rozbělesy. Závěrečná zpráva. Praha: AQUATEST, Stavební geologie a.s. Praha.
SKOŘEPA, Jaroslav, Petr CHARVÁT, Markéta HRKALOVÁ, Zdeněk JEZERSKÝ, Lucia LENCSESOVÁ, Kamil NEŠETŘIL, Ondřej NOL, Aleš PACL, Věra PĚKNÁ, Ivan PERGLER a Tomáš VRÁNEK, 2009. Hydrogeologický monitoring a posouzení pohybu podzemních vod na hranicích Polské, Německé a České republiky v povodí toků Horní Ploučnice, Nisy a Smědé, závěrečná zpráva 2008/2009. Číslo úkolu: J241080220000. Praha: AQUATEST a.s.
WIDDOWSON, Mark A., Eduardo III MENDEZ, Steven BRAUNER, Francis H. CHAPELLE a Clifton C. CASEY, 2008. Natural Attenuation Software (NAS). USA: VirginiaTech, USGS, NAVFAC.
WILSON, R.D., S.F. THORNTON, A. HUETTMANN, M. GUTIERREZ-NERI a H. SLENDERS, 2005. CoronaScreen : Process-based models for natural attenuation assessment: guidance for the application of NA assessment screening models. 2005. University of Sheffield, UK; TNO Institute of Environmental Sciences, The Netherlands. https://www.sheffield.ac.uk/media/19256/download?attachment
ZHENG, Chunmiao, 1998. MT3DMS : A Modular 3-D Multi-Species Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems. USA: University of Alabama.
ZHOU, Yangxiao a Henk HAITJEMA, 2012. Approximate solutions for radial travel time and capture zone in unconfined aquifers. Ground Water. 50(5), 799–803. ISSN 1745-6584. 10.1111/j.1745-6584.2011.00883.x