Obsah
Alternativní jednoduché modely podzemní vody
Abstrakt
Epistemologická nejistota modelů podzemní vody se projevuje v nejistotě koncepčního modelu, a to zejména ve struktuře modelu. S ní je možno se vyrovnat využitím více (i velmi jednoduchých) koncepčních modelů založených na různých přístupech či předpokladech. Práce shrnuje existující klasifikace nejistot (zejm. koncepčního modelu) a navrhuje novou klasifikaci využití modelů. Prezentované případové studie srovnávají jednoduché a komplexní modely, testují alternativní hypotézy sadou jednoduchých modelů či představují alternativní prediktivní modely. Taková strategie se ukazuje jako velmi účelná obzvláště při nedostatku adekvátních vstupních dat, kdy není možné model validovat. Obhajitelnost modelů je semikvantitativně vyhodnocena.
Klíčová slova
hydrogeologie, podzemní voda, matematický model, nejistota, epistemologická nejistota, nejednoznačnost, koncepční model, struktura modelu, ekvifinalita, alternativní modely, jednoduchost
Abstract
Epistemological uncertainty of groundwater models is reflected in the conceptual model uncertainty, especially in the model structure. It is possible to cope with it by using more (even very simple) conceptual models based on different approaches or assumptions. The thesis summarizes the existing classifications of uncertainty (esp. that of conceptual model), and proposes a new classification of model usage. The presented case studies compare simple and complex models, test alternative hypotheses by a set of simple models or represent alternative predictive models. Such a strategy is very effective especially in the absence of adequate input data when it is not possible to validate the model. Tenability of the models is evaluated semi-quantitatively.
Keywords
hydrogeology, groundwater, mathematical model, uncertainty, epistemic uncertainty, ambiguity, conceptual model, model structure, equifinality, multiple model ensemble, multimodel approach, multimodel analysis, parsimony, simplicity
Úvod
Celý profesní život se autor předkládané práce zabývá modelováním podzemní vody a po počáteční fascinaci komplexními modely zjišťoval, že složité modely s vysokým počtem stupňů volnosti (parametrů) často nejsou užitečným podkladem pro porozumění probíhajícím procesům ani pro rozhodování – mimojiné proto, že často nejsou adekvátně podpořeny daty. Navíc je obtížné je sestavit a výsledky vyhodnotit. Předkládaná práce proto demonstruje užitečnost využití více jednoduchých modelů. Pro usnadnění jejich tvorby byl vyvinut informační systém HgIS. Pro řešení běžných hydrogeologických úloh (jejichž charakteristikou je často nedostatek adekvátních vstupních dat) tak práce nabízí strategii (více jednoduchých modelů) a nástroj (HgIS).
Při modelování podzemní vody čelíme nejistotě ve výsledcích modelu. Ta je dána nejistotou vstupních dat a nejistotou naší interpretace těchto dat (tzv. epistemologická nejistota – tzn. nedostatečné pochopení fungování systému). Je dobrou praxí hodnotit nejistotu predikcí na základě shody modelu s validačními daty. Skutečná nejistota je však často hlubší – podzemí totiž není přístupné přímému pozorování, a proto často bývá důležitější nejistota interpretací. Tyto úvahy vyžadují jednoznačné vymezení pojmů, které však nejsou v literatuře používány jednoznačně – na začátku je proto představeno shrnutí existujících klasifikací nejistot. Je zde definována epistemologická nejistota a její projevy: nejistota koncepčního modelu a nejistota struktury modelu. Pro vypořádání se s takovou nejistotou je v práci obhajována a využita strategie více jednoduchých modelů, které jsou založeny na různých přístupech či předpokladech. Tyto jednoduché modely mohou být formulovány jako testování hypotéz a jednoznačně snižovat nejistotu porozumění fungování studovaného systému. Využití modelů pro testování hypotéz je spolu s dalšími uvedeno v navržené klasifikaci využití modelů (kapitola Formulace zvoleného přístupu). V práci je diskutováno použití principu ekvifinality a tohoto pojmu v oblasti modelování podzemní vody. Práce vychází z článků zabývajících se zejm. hydrogeologií, i když principy využití alternativních jednoduchých modelů jsou platné pro různé obory.
V kapitole Případové studie je prezentováno využití alternativních jednoduchých modelů v modelování různých hydrogeologických úloh. Jedna úloha je řešena více modely, které jsou založeny na různých přístupech a předpokladech. Vysoká nejistota modelů je dána nedostatkem adekvátních vstupních dat (a tedy i informací a znalostí o lokalitě – tak i dále). Proto také nebylo možno výsledky modelů kalibrovat ani validovat, ale případně pouze srovnávat výsledky jednotlivých modelů mezi sebou. Prezentované případové studie srovnávají jednoduché a komplexní modely, testují alternativní hypotézy sadou jednoduchých modelů či představují alternativní prediktivní modely. Obhajitelnost modelů je semikvantitativně vyhodnocena s využitím metodiky nalezené v literatuře (kapitola Hodnocení nejistoty koncepčního modelu podle Refsgaarda et al. 2006).
Pro rychlou orientaci je tedy možno říci, že tato práce představuje teoretický úvod do problematiky nejistoty, alternativních modelů a jednoduchosti v modelování. Kapitola Případové studie přináší ukázky praktického využití principů z předchozí části na modelech různých lokalit. Výsledkem práce není formální metodika – uvedené principy je však možno uplatnit při zpracování dalších případových studií.
Dva dříve zvažované názvy předkládané práce charakterizují stručně její náplň: Kombinace principiálně odlišných jednoduchých modelů – případové studie a nástroj. Ekvifinalita v modelování podzemní vody.
Tato práce má do jisté míry syntetický charakter a může být tudíž obtížněji uchopitelná. Práce cituje velké množství literatury a nezachází příliš do detailů. Pro úplnost obsahuje práce převzaté obrázky a citáty, které jsou uvedeny v původním jazyce (angličtině) bez překladu.
Východiska práce
Cíle práce
- Teoreticky vyhodnotit důsledky nedostatečných informací pro tvorbu modelů podzemní vody. Popsat strategii alternativních jednoduchých modelů pro modelování nedostatečně definovaných hydrogeologických systémů.
- Demonstrovat užitečnost strategie na případových studiích v terénním měřítku – včetně těch, které testují hypotézy.
- Nejen s pomocí těchto případových studií zformulovat požadavky na informační systém, který by podporoval formulování koncepčních modelů a umožňoval implementaci jednoduchých procedurálních (tj. výpočetních) modelů.
- Požadavky analyzovat, navrhnout informační systém a využít jej v praxi.
- Prověřit, zda přístupy a nástroje business intelligence jsou vhodné pro řešení této problematiky.
Matematické modely podzemní vody
Každý model je abstrakcí, zjednodušením a interpretací reality (Refsgaard et al. 2006). Model také může být zjednodušená teorie (Refsgaard a Henriksen 2004). Model tedy může být „black box“, teorie však nemůže být „black box“.
Podle Bevena a Younga (2013) neexistují (alespoň zatím) modely v hydrologii plně založené na fyzikálních principech. Autor předkládané práce se domnívá, že se v hydrogeologické praxi často přeceňuje fyzikální pojetí úlohy (obecněji pojetí založené na popisu procesů – process-based), ačkoliv v důsledku heterogenit a měřítka není toto pojetí plně možné (i když stále více možné než v případě hydrologie povodí)1). Alternativou k těmto redukcionistickým modelům (deterministic reductionism) jsou techniky založené na datech (Young 1998; Clark et al. 2011) – data-driven models (k nim lze v podstatě řadit i empirické modely). Pro modely podzemní vody byly využity metody jako soft computing, strojové učení a data mining a to například: využití neuronových sítí (Coulibaly et al. 2001; Michael et al. 2005), dynamiky systémů (Roach a Tidwell 2009), rozhodovacích stromů atd. (Litaor et al. 2010; Rapantová et al. 2012; Farrell et al. 2007). Deep learning pro hydrologii a hydrogeologii shrnuje (Marçais a de Dreuzy 2017). Využití těchto přístupů pro oblast vodních zdrojů shrnuje review paper (Razavi et al. 2012). Přístupy prezentované v předkládané práci jsou většinou fyzikálně založené modely (process-based), i když jejich matematická formulace není vždy plně korektní. Většímu využití alternativních strategií modelování však může přispět informační systém HgIS.
V předkládané práci je uváděna terminologie týkající se matematického modelování. Pojmy jsou jednoduše a jednoznačně vysvětleny v článku (Beven a Young 2013). Jedná se o pojmy týkající se rozčlenění modelů (lumped × distributed, deterministic × stochastic, inductive × deductive, black-box × process-based, inductive × deductive), nejistoty (aleatory × epistemic; conditional validation, split-record test, postaudit) a typů modelování (simulation, ex-ante forecasting, ex-post forecasting, hindcasting a projection – ‘‘what-if’’ simulations). Pojmy tedy nebudou v předkládané práci dále objasňovány.
Fáze tvorby modelu, koncepční model
Tabulka 1 ukazuje fáze tvorby modelu podle různých autorů. Dále je používána terminologie Bevena (2001; 2012), podle níž percepční model představuje subjektivní porozumění (vnímání) probíhajícím procesům, které může být čistě kvalitativní. Koncepční model je jeho konkrétní zjednodušené vyjádření (např. řídicí rovnice, doména, okrajové podmínky, parametry), které se týká konkrétní lokality. Procedurální (tj. výpočetní) model je pak implementace koncepčního modelu v konkrétním software (sw) bez ohledu na to, zda jde o numerické, či analytické řešení.
Tabulka 1: Fáze tvorby modelu – srovnání terminologií
| Beven (2001, 2012) | Gupta et al. (2012) | ||
|---|---|---|---|
| Fáze | Charakter fáze | Fáze | Charakter fáze |
| Percepční model | Porozumění fungování systému – i bez vnímatelného vyjádření | Percepční model | Představy o fungování systému + interpretace dat |
| Koncepční model | Zjednodušení percepčního modelu (např. nákres) | ||
| Koncepční model | Rovnice a parametry – zjednodušení a formalizace percepčního modelu | Matematický model | Rovnice a parametry – formalizace koncepčního modelu |
| Procedurální model | Software | Výpočetní model (computational) | Numerické či analytické řešení |
Další pohled na fáze tvorby modelu uvádí Refsgaard a Henriksen (2004) – viz obrázek 1.
Ověřování modelu má tři stupně – mohli bychom říci s klesající silou pojmu (Refsgaard a Henriksen 2004):
- verifikace (tak striktní ověření se může vztahovat např. na samotné analytické či numerické řešení a jeho implementaci),
- validace (srovnání výsledků modelu konkrétní lokality s měřeními) a
- potvrzení (confirmation – pro koncepční model).
Validace nespočívá v testování úplnosti modelu či jeho absolutní pravdivosti (jako u vědecké teorie), ale ověřuje, zda je model přijatelný pro zvolený účel. U koncepčního modelu je vhodné spíše než o validaci mluvit o potvrzení (confirmation) – obrázek 1. Každý koncepční model je zjednodušením probíhajících procesů a může být proto vyvrácen (falzifikován), pokud jej prozkoumáme do dostatečného detailu a uplatníme na něj dostatečně vysoká kritéria (Refsgaard a Henriksen 2004). Tvorbou hydrogeologických koncepčních modelů se zabývají z praktického hlediska Krešić a Mikszewski (2012).
 Obrázek 1: Základní pojmy z oblasti modelování. Zdroj: Refsgaard a Henriksen (2004)
Obrázek 1: Základní pojmy z oblasti modelování. Zdroj: Refsgaard a Henriksen (2004)
Klasifikace a hodnocení nejistoty (modelu)
Výsledky matematického modelu nemají význam, pokud není zřejmá jejich důvěryhodnost. Proto je vhodné ověřovat model a hodnotit nejistotu modelu. Kreye et al. (2011) uvádí klasifikaci nejistot včetně nejistot modelu. Z klasifikace plyne rozdíl mezi nejistotou koncepčního modelu a strukturní nejistotou modelu, což jsou pojmy, které jsou v literatuře hojně používány. Z článku je převzata tabulka 2, jež byla doplněna dalšími údaji z citované literatury. Hvězdička (*) naznačuje druhy nejistot důležité z hlediska této disertace.
Klasifikace nejistoty podle pěti vrstev (podle původího textu disertace tabulka 2)
Povaha (Nature)
Všeobecná charakteristika nejistoty
- stochastická (aleatory) čili ontologická (daná inherentní variabilitou)
- variabilita (nahodilé chování systému) – Warmink et al. (2010)
- nejednoznačnost – ambiguity (rozpory v informacích) – Warmink et al. (2010)
- epistemologická čili systematická (daná nedokonalou znalostí)
Příčina (Cause)
Důvod či zdroj nejistoty:
- nedostatek porozumění *
- nejednoznačnost
- lidská činnost
Úroveň (Level)
Závažnost nejistoty, např.:
- množství dostupných informací
- množství informací chybících pro určitý popis stavu a procesů *
Podle Warmink et al. (2010) – viz barvy na obrázku 3:
- statistická (nejistota může být kvantifikována)
- nejistota scénářů (nejistota může být popsána pomocí alternativ chování systému) *
- kvalitativní (nejistota může být popsána) – neuvádí Walker et al. (2003)
- rozpoznaná neznalost (nejistota nemůže být popsána)
- naprostá neznalost (Walker et al. 2003)
Projev (Manifestation), Umístění (Location)
Místo v procesu, kde se nejistota projeví (Walker et al. 2003; Warmink et al. 2010):
- nejistota kontextu (z vnějšku modelu – co model nepostihuje – např. účel)
- endogenní (z vnitřku organizace)
- exogenní (z vnějšku organizace)
- nejistota dat – vstupů (Warmink et al. 2010), pozorování
- neúplnost dat (mezery v dostupných datech)
- nepřesnost dat (nepřesnost či nespolehlivost dostupných dat)
- variabilita dat (různé možné alternativy) *
- nejistota modelu
- koncepční (zjednodušení v koncepčním modelu) *
- nejistota struktury modelu (neadekvátnost či diskrepance modelu) – celkový nedostatek porozumění *
- opomenutí procesů (řídicí rovnice)
- nejistota v definici domény (rozsahu modelu) a okrajových podmínek
- geologická nejistota (Refsgaard et al. 2012)
- …
- nejistota parametrů modelu
- přesné parametry – např. π (Walker et al. 2003)
- fixní parametry – např. gravitační zrychlení (Walker et al. 2003)
- a priori zvolené parametry – obtížné identifikovat (Walker et al. 2003) – nepodmíněná nejistota (Singh et al. 2010)
- kalibrované parametry – např. transmisivita (Walker et al. 2003) – podmíněná nejistota (Singh et al. 2010)
Podle Singh et al. (2010):- nejistota kalibrace z důvodu chyb v datech
- nejednoznačnost z důvodu necitlivosti parametrů
- nejednoznačnost z důvodu korelace parametrů
- technická stránka modelu (Walker et al. 2003):
- matematická čili algoritmická (zjednodušení v matematickém vyjádření)
- výpočetní čili numerická (zjednodušení ve výpočetní metodě)
- fenomenologická nejistota (neznámé události v budoucnosti)
Vyjádření (Expression)
Způsob jak je nejistota vyjádřena či sdělena. Může být:
- kvantitativní (měřitelná)
- kvalitativní (neměřitelná).
Metodiku pro rozčlenění konkrétních zdrojů nejistot uvádí Warmink et al. (2010), jež vychází z článku (Walker et al. 2003).
Klasifikaci nejistot v modelech uvádí Singh et al. (2010) – obrázek 2.
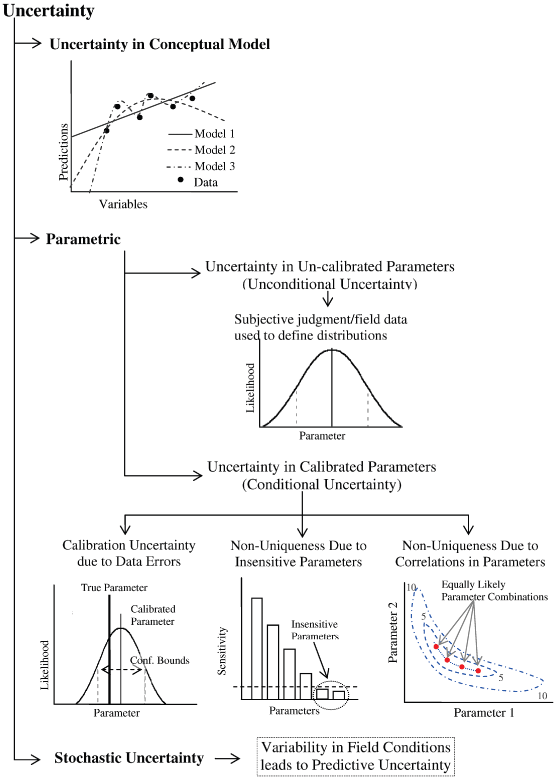 Obrázek 2: Schéma různých typů nejistoty v modelech (Singh et al. 2010, s. 702)
Obrázek 2: Schéma různých typů nejistoty v modelech (Singh et al. 2010, s. 702)
Další klasifikaci nejistot (podle zdroje nejistoty) uvádí Uusitalo et al. (2015):
- Přirozená nahodilost
- Nahodilá chyba měření
- Systematická chyba měření
- Přirozená variabilita (změna v čase a prostoru)
- Nejistota modelu
- Subjektivní úsudek
S nejistotou v modelech je možno se vyrovnat pomocí metod jako je Monte Carlo, stochastických / pravděpodobnostních modelů, variantních výpočtů – alternativních scénářů (Mahmoud et al. 2009), alternativních koncepčních modelů a dalších metod. Základní dvě skupiny metod kvantifikace nejistot jsou propagace nejistot a řešení inverzního problému. Metody pro hodnocení nejistoty jsou zároveň jedním z přístupů pro vypořádání se (coping) s nejistotou.
Existuje mnoho metodik pro hodnocení nejistot, které uvádí Refsgaard et al. (2007):
- Data uncertainty engine (DUE) – Brown et al. (2005)
- Rovnice propagace chyby (Mandel 1984)
- Dotazování expertů (Expert elicitation) – např. pomocí strukturovaného dotazníku
- Rozšířené recenzní řízení (recenze zainteresovanými subjekty)
- Inverzní modelování (odhad parametrů)
- Inverzní modelování (nejistota predikcí)
- Analýza Monte Carlo
- Simulace více modely – modely s odlišnou strukturou
- NUSAP (van der Sluijs et al. 2005)
- Zajištění kvality (QA) – využití metodiky pro vhodnou aplikaci modelů
- Analýza scénářů – scénáře budoucího vývoje
- Analýza citlivosti
- Účast zainteresovaných subjektů (stakeholder involvement)
- Matice nejistot (Refsgaard et al. 2007), tabulka 3.
V případě nedostatku dat pro kalibraci a validaci modelu je třeba využívat semikvantitativní a kvalitativní hodnocení jako je NUSAP či matice rodokmenu (pedigree matrix) – jednodušeji řečeno matice nejistot. Hodnocení podle matice nejistot (Refsgaard et al. 2007) – tabulka 3 – vychází (podobně jako klasifikace nejistot – viz tabulka 2) taktéž z Walkera et al. (2003), ale zobrazení ve formě matice umožňuje prakticky hodnotit nejistotu. Ukazuje, že jednotlivé klasifikace nejistot se nevylučují. Povahu (nature) je možno chápat jako třetí dimenzi. Pojmy jsou patrné z obrázku 3.
Tabulka 3: Matice nejistot (Refsgaard et al. 2007, s. 1548)
| Source of uncertainty | Taxonomy (types of uncertainty) | Nature | |||||
|---|---|---|---|---|---|---|---|
| Context | Natural, technological, social, political | Statistic uncertainty | Scenario uncertainty | Qualitative uncertainty | Recognized ignorance | Epistemic uncertainty | Stochastic uncertainty |
| Inputs | System data | ||||||
| Driving forces | |||||||
| Model | Model structure | ||||||
| Technical | |||||||
| Parameters | |||||||
| Model outputs | |||||||
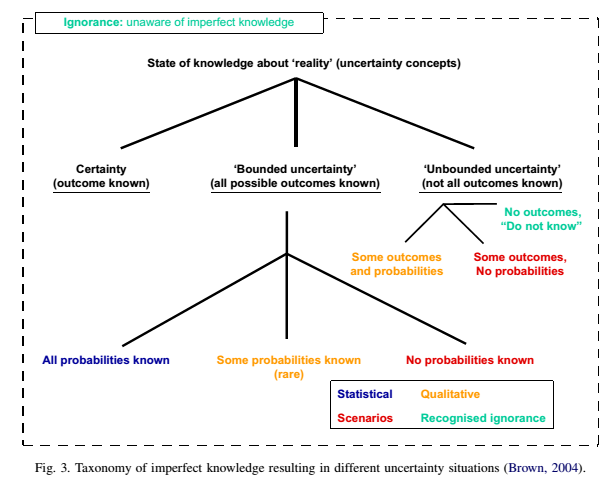 Obrázek 3: Klasifikace nedokonalého poznání. Zdroj: Brown (2004), citováno dle Refsgaard et al. (2007, s. 1547)
Obrázek 3: Klasifikace nedokonalého poznání. Zdroj: Brown (2004), citováno dle Refsgaard et al. (2007, s. 1547)
Příklad hodnocení podle metodiky NUSAP (van der Sluijs et al. 2005) naznačuje tabulka 4 a obrázek 4. Celková nejistota je hodnocena pomocí skóre, které je součtem dílčích skóre.
Tabulka 4: Matice rodokmenu (pedigree matrix) pro monitoring emisí (van der Sluijs et al. 2005)
| Skóre | Reprezentativnost | Podkladová data | Metoda | Validace |
|---|---|---|---|---|
| 4 | Přesná shoda | Přímá měření na velkých vzorcích | Nejlepší dostupná metoda | Porovnáno s nezávislými měřeními stejné proměnné |
| 3 | Dobrá shoda | Přímá měření na malých vzorcích | Spolehlivá a všeobecně přijímaná metoda | Porovnáno s nezávislými měřeními úzce související proměnné |
| 2 | Dobře koreluje | Modelovaná či odvozená data | Přijímaná teorie nepovažovaná za spolehlivou | Porovnáno s nikoliv nezávislými měřeními |
| 1 | Slabě koreluje | Expertní odhad, empirická pravidla | Předběžné metody s neznámou spolehlivostí | Slabá/nepřímá validace |
| 0 | Bez jasné vazby | Čistá spekulace | Nespolehlivé metody | Bez validace |
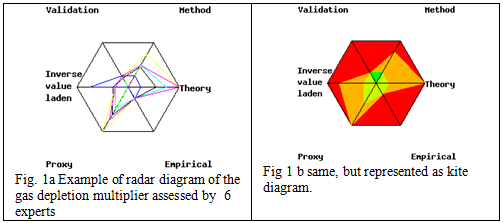 Obrázek 4: Metodika NUSAP (van der Sluijs et al. 2005)
Obrázek 4: Metodika NUSAP (van der Sluijs et al. 2005)
Metodika NUSAP je velmi podobná matici rodokmenu (pedigree) (Refsgaard et al. 2006), o které je pojednáno níže v souvislosti s nejistotou koncepčního modelu.
Uusitalo et al. (2015) uvádí přístupy pro hodnocení nejistoty v modelech pro podporu rozhodování:
- Expertní hodnocení
- Analýza citlivosti modelu
- Emulace modelu (Model emulation: meta-model, surrogate model, reduced model, proxy model, lower fidelity model, behavioral model či black-box model) – nízkoúrovňová aproximace komplexnějšího modelu dávající dobré predikce i když jeho formulace není fyzikálně zcela korektní. Dobrým příkladem v hydrogeologii je přístup „compartmental–spatial system dynamics“ (Roach a Tidwell 2009).
- Časová či prostorová variabilita v deterministických modelech (např. extrémní měřené hodnoty použít jako hodnoty parametrů modelu)
- Více modelů
- Přístupy založené na datech (data-based approaches) – např. nalezení analogií
Strategie zvolená v předkládané práci v podstatě odpovídá kombinaci „emulace modelu“ a „více modelů“. Je to však značně zjednodušené tvrzení, protože „emulace modelu“ není to stejné jako jednoduchý model.
Významný zdroj nejistoty – epistemologická nejistota
Jak ukazuje tabulka 2, dělíme nejistotu podle povahy (nature) na stochastickou (aleatory) a epistemologickou (epistemic). Epistemologická nejistota se může týkat toho, které jevy určují chování studovaného systému (omezené porozumění komplexnosti přírodních dějů). Její důsledky proto mohou být často závažnější než důsledky stochastické nejistoty. Podle Bevena a Younga (2013) je nejistota povahy spíš epistemologické než stochastické.
Často jsou využívány statistické metody [Level: statistical – viz tabulka 2 (Warmink et al. 2010)] hodnocení nejistoty, které jsou vhodné pro odhad stochastické nejistoty, ale není snadné hodnotit těmito metodami epistemologickou nejistotu (Beven a Young 2013).
Beven a Westerberg (2011) se zabývají zavádějícími úseky v hydrologických časových řadách či v datech. Článek ukazuje na význam epistemologické nejistoty a na to, že statistické metody jsou pro její hodnocení nevhodné: „These classical measures effectively assume, however, that the sources of error are essentially stochastic or aleatory in nature, whereas disinformation is a form of knowledge or epistemic error. They assume that every residual is informative in conditioning the model parameters and uncertainty.“ (Beven a Westerberg 2011, s. 1676)
Projev epistemologické nejistoty – nejistota koncepčního modelu
Epistemologická nejistota se pak v modelu projevuje jako nejistota koncepčního modelu (uncertainty in conceptual model), a to konkrétně jako strukturní nejistota (nejistota ohledně struktury modelu – structural uncertainty). Neadekvátní struktura modelu je pro předpovědi modelu často mnohem důležitější než nepřesnost parametrů modelu (Neuman a Wierenga 2003, s. E-4 – tj. 302).
Nejistotu koncepčního modelu je možno kvantifikovat a hodnotit různými způsoby, které shrnul Refsgaard et al. (2006 Fig. 2) v následující klasifikaci:
Jsou dostupná data pro validaci modelu?
- Existují data, která je možno přímo srovnat s výsledky modelu (interpolace):
- Zvýšit nejistotu parametrů (kompenzace strukturní nejistoty – Statistická nejistota běžně charakterizující nepřesnost tak obsáhne další rozměry nejistoty včetně epistemologické).
- Odhadnout strukturní člen
(nejistota výstupů ‒ nejistota vstupů = strukturní nejistota).
- Neexistují data, která je možno přímo srovnat s výsledky modelu (extrapolace):
- Více koncepčních modelů:
- Alespoň nějaká data (differential split-sample test: validační data odpovídají jiným podmínkám než data, na které byl model kalibrován)
- Žádná data (proxy basin case: model je verifikován na datech z jiného povodí – lokality)
- Názor expertů
- Analýza rodokmenu (pedigree):
- NUSAP (van der Sluijs et al. 2005) – tabulka 4 a obrázek 4
- Matice rodokmenu (pedigree) (Refsgaard et al. 2006) – viz tabulka 5
Matice rodokmenu (pedigree matrix) Refsgaarda et al. (2006) přestavuje kvalitativní či semikvantitativní hodnocení nejistoty koncepčního modelu (tabulka 5). Hodnocení je využito pro případové studie (kapitola Hodnocení nejistoty koncepčního modelu podle Refsgaarda et al. 2006). Kvůli jisté vágnosti se zde nehovoří o nejistotě, ale o obhajitelnosti (tenability) – viz potvrzení koncepčního modelu v kapitole Fáze tvorby modelu, koncepční model (Refsgaard a Henriksen 2004). Uvedená práce navazuje na analýzu NUSAP (van der Sluijs et al. 2005), tabulka 5 je proto velmi podobná tabulce 4.
Tabulka 5: Matice rodokmenu (pedigree matrix) pro hodnocení obhajitelnosti koncepčního modelu (Refsgaard et al. 2006, s. 1593)
| Skóre | Podložení empirickými důkazy | Teoretické porozumění | Reprezentace porozumění procesům | Věrohodnost | Shoda názorů odborníků | |
|---|---|---|---|---|---|---|
| Reprezentativnost | Kvalita a kvantita | |||||
| 4 | Přesně odpovídá hodnotami i významem | Řízené experimenty a přímá měření na velkých vzorcích | Prověřená teorie | Rovnice do detailu popisují mechanismus procesů | Vysoce věrohodný | Všichni kromě bláznů |
| 3 | Dobře odpovídá hodnotami i významem | Archivní/terénní data, neřízené experimenty, malé vzorky, přímá měření | Přijímaná teorie | Rovnice přijatelně popisují mechanismus procesů | Rozumně věrohodný | Všichni kromě kverulantů |
| 2 | Dobrá korelace ne úplně stejných veličin | Modelovaná či odvozená data, nepřímá měření | Přijímaná teorie nepovažovaná za spolehlivou | Metamodel s agregovanými parametry | Poněkud věrohodný | Konkurenční školy |
| 1 | Slabá korelace, ale srovnatelná veličina | Expertní odhad, empirická pravidla | Předběžná teorie | Grey box model | Málo věrohodný | Obor „v plenkách“ |
| 0 | Nekorelovány a bez přímé vazby | Čistá spekulace | Čistá spekulace | Black box model | Nevěrohodný | Bez názoru |
Při hodnocení nejistoty koncepčního modelu je podle Refsgaarda et al. (2006) vhodné postupovat následujícím způsobem:
Protokol pro hodnocení nejistoty koncepčního modelu
- Formulovat koncepční model.
- Sestavit a nakalibrovat model.
- Je koncepční model dostatečný? (Pokud ne – návrat do bodu 1)
- Provést validační test a přijmout/zamítnout modely.
- Vyhodnotit obhajitelnost a úplnost koncepčních modelů.
- Vypočítat predikce a vyhodnotit nejistoty.
Alternativní koncepční modely
Jako jedna z úrovní (level) nejistoty (tabulka 2) je uváděna úroveň scénářů (scenario) – nejistota nemůže být kvantifikována statisticky, ale může být vyjádřena pomocí alternativních popisů (koncepčních modelů). Tato úroveň nejistoty je běžná při řešení praktických hydrogeologických úloh, jako jsou mj. předkládané případové studie. Alternativní koncepční modely snižují dopady faktu, že tvorba koncepčního modelu je zatížena subjektivním vnímáním autora (Bredehoeft 2005).
Význam alternativních modelů ilustrují citáty:
„Evolutionary science suggests that any single diagnostic path along a model evolution tree can lead prematurely to a dead end (locally optimal solution), while some previously rejected branch of the tree may ultimately lead to a more satisfactory solution. Topdown investigations are therefore likely to achieve more power by maintaining several parallel lines of investigation beginning with multiple prior conceptualizations.“ (Gupta et al. 2012, s. 11)
„Equifinality may signal the end of the dead-end track of distributed modelling.“ (Savenije 2001, s. 2837)
Refsgaard et al. (2007, s. 1550) uvádí pro simulace za využití více modelů: „The main advantages of this method are that the effects of alternative model structures can be analysed explicitly and that the robustness of the model predictions increases. An important uncertainty is that we cannot be sure whether we have adequately sampled the relevant space of plausible models and that important plausible model structures could be overlooked.”
„We have noted earlier that there is uncertainty not only about the parameter values that should enter into a given model (as characterized by its structure), but also about the very structure (conceptual and mathematical) of the model that should represent the hydrologic system of interest. The traditional approach to model uncertainty analysis, which considers only a single deterministic model structure, fails to adequately sample the complete space of plausible hydrologic models. As such, it is prone to modeling bias and underestimation of model uncertainty.” (Neuman a Wierenga 2003, s. E-5 – tj. 303)
Názory praktiků a zadavatelů modelů popisuje zajímavě Poeter (2007, s. 390): „I found loud resistance to and quiet support for using multiple conceptual models in the hydrologic community. For the most part, only one conceptual model is used in projects at this time, so consideration of even just one more alternative is a good start toward better defining the full uncertainty. Once it becomes apparent that alternative models can provide acceptable fit to the field data and yet produce quite different values for predictions of interest in the decision process, appetites will be whetted for considering more alternatives. Following the lecture, some hydrologic consultants would say that regulators would not stand for such “wishy-washy” work where the system was so unknown that it is not possible to select one “best” model. Some would confide that they explored alternative conceptual models but were hesitant to present the results because they would appear to be an incompetent hydrologist due to their uncertainty. At some of the same lectures, regulators would say multiple models are exactly what is needed. They stated that they frankly did not believe the uncertainty was as small as indicated by the values typically presented to them.”
To, že alternativní koncepční modely lépe vyjadřují nejistotu, uvádí Poeter a Anderson (2005, s. 597): „We often find that prediction uncertainty is larger across the range of potential models than that which arises from the misfit and insensitivity of any one optimized model, even to the extent that confidence intervals on predictions from some of the models may not include the values predicted by others.”
Bredehoeft (2005) uvádí, že mnozí autoři navrhují využití alternativních koncepčních modelů, které jsou testovány, či je z nich vybrán ten nejlepší. Uvádí však, že nikdy nezaznamenal tento přístup uskutečněný v praxi, protože modeláři pracují s jedním koncepčním modelem, který mění až v případě, kdy jej není možné nakalibrovat.2) Předkládaná práce naopak ukazuje, jak je možno uplatnit alternativní koncepční modely v praxi – totiž používat (alespoň v první fázi) více jednoduchých modelů. S pomocí informačního systému HgIS či jiných vhodných nástrojů je tvorba koncepčních modelů snazší, a je tak možno jich prakticky vytvořit více.
Využitím alternativních modelů pro rozhodování se zabývá zásadní práce (Ferré 2017). Má pomoci přehodnotit chybné předpoklady zainteresovaných osob (stakeholders). Užívá pojmy jako: multiple-narrative approaches, teams of rival models, advocacy models, consequential models.
Clark et al. (2015a; 2015b) vyvinuli framework pro tvorbu alternativních modelů: Structure for Unifying Multiple Modeling Alternatives (SUMMA) – viz obrázek 5. Jeho cílem je mj. hodnotit alternativní representace procesů na různých měřítkách a s různou mírou zjednodušení. Zdrojové kódy jsou veřejně dostupné (GitHub).
 Obrázek 5: Alternativní reprezentace hydrologických procesů (Clark et al. 2015a; 2015b)
Obrázek 5: Alternativní reprezentace hydrologických procesů (Clark et al. 2015a; 2015b)
Alternativní modely je možno srovnávat a hodnotit. Jedním z kvantitativních přístupů je průměrování modelů (model averaging). Jednou z takových metod je GLUE – Generalized Likelihood Uncertainty Estimation (Beven 2006). Srovnání různých metod průměrování modelů podzemní vody uvádí Singh et al. (2010).
Uusitalo et al. (2015) uvádí pojem „ensemble modelling“: „While qualitative analysis of modelling results can give us an idea of the extent of uncertainty related to them, various ways have been proposed in the literature to combine several models. The term ensemble modelling is used both for running a single model multiple times with different sets of initial values (single model ensemble), and for using multiple models (multiple model ensemble). Ensemble modelling has mainly been used in two ways: to produce one “best” predictive model and to evaluate the predictive uncertainty“. „Ensemble modeling“ v hydrologii používá například Breuer et al. (2009). Publikace, které by používaly pojem ensemble modeling pro modelování podzemní vody, nebyly nalezeny.
Hodnocení na základě více modelů se používá v různých oborech. Například algoritmus Náhodný les (Random forest) taktéž vychází z více modelů (klasifikačních stromů). Jako správná klasifikace se pak zvolí ta, která je výsledkem nejvíce stromů (hlasování).
Volba nejlepšího modelu – testování hypotéz
Již geolog Chamberlin (1890) vyzýval k tvorbě více pracovních hypotéz jakožto strategii pro rychlý pokrok v porozumění praktickým i teoretickým problémům. Využití více modelů jako testovatelných pracovních hypotéz komentuje Clark et al. (2011).
Důležitost využití modelů jako hypotéz, jež jsou testovány, zdůrazňují Beven a Young (2013): „We normally learn more from falsification than from (conditional) model validation. Falsification implies some improvement is required, either in the data that is being used to drive and evaluate the model or in the model structure itself. However, testing models as hypotheses in this manner is difficult in hydrology and other areas of environmental science because of the inherent epistemic nature of many sources of uncertainty.”
Schéma na obrázku 5 ukazuje metodiku pro testování koncepčních modelů a sad parametrů (Beven 2002) – testování hypotéz. Na počátku jsou uvažovány různé modely, z nichž postupně vylučujeme ty, jež jsou fyzikálně nemožné, jež dávají nerealistické výsledky a jež jsou v příkrém rozporu s pozorováními. Se zbylými modely je možno počítat predikce. Variabilita výsledků těchto modelů ukazuje nejistotu predikce.
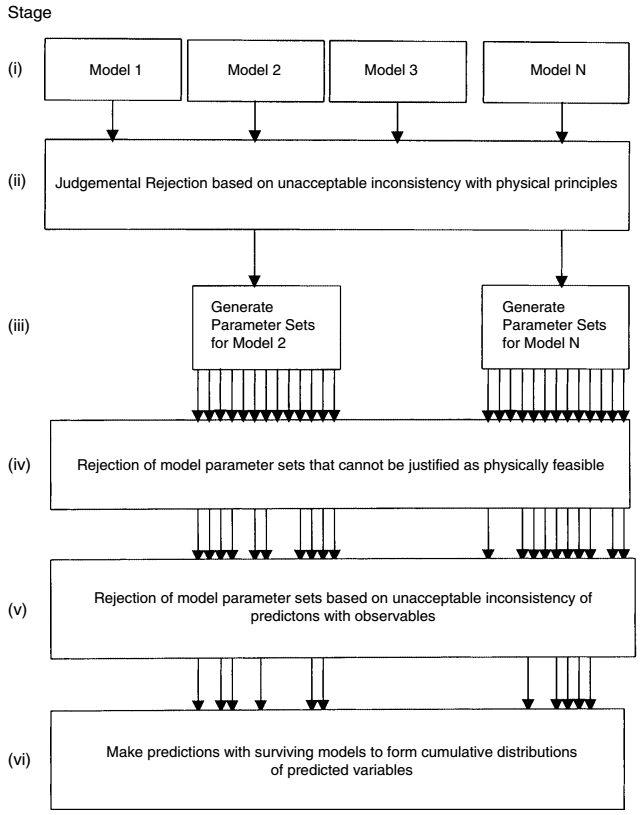 Obrázek 6: Testování modelů (Beven 2002)
Obrázek 6: Testování modelů (Beven 2002)
Testování hypotéz je nesmírně důležité, protože představuje jádro metodologie vědy. Vědecká metoda spočívá ve formulaci hypotéz, které se pokoušíme vyvrátit – falzifikovat (Popper 1997). To, že pozorování odpovídají teorii, ještě nedokazuje pravdivost teorie. Stejně tak shoda modelu s pozorováním nepotvrzuje, že předpoklady či další předpovědi modelu jsou správné. Vyvrácení chybné hypotézy je však prokazatelný výsledek. Nadneseně lze říci, že vyvrácení koncepčního modelu, vyvrácení vědecké hypotézy a změna paradigmatu – vědecká revoluce (Kuhn 1970; 2008) – jsou podobné události na různých měřítcích vědy.
Výše uvedené metody nejsou však v hydrogeologické komunitě zcela samozřejmé. Článek zabývající se modelováním podzemních vod (Bredehoeft 2005) nepracuje s pojmy jako hypotéza a jejich vyvracení. Místo toho změnu koncepčního modelu označuje jako překvapení (surprise). K němu dojde podle zkušeností autora článku u 20–30 % případů. Autor se nesnaží koncepční modely vyvrátit. K jejich nahrazení dojde až ve chvíli, kdy se mu nedaří stávající koncepční model ani podpořit.
Počáteční koncepční model obsahuje strukturu a počáteční hodnoty parametrů. Při kalibraci jsou upraveny parametry. Takový model může být dále validován konfrontací s nezávislými pozorováními – pokud možno jiné veličiny, než na kterou byl model kalibrován. Takový postup je možno chápat jako testování hypotézy, protože ve fázi kalibrace i validace se může ukázat, že ani model s optimalizovanými parametry není schopen adekvátně reprodukovat chování systému. Je tedy možno tvrdit, že testování hypotéz je součást standardní modelářské praxe. Autor předkládané práce se domnívá, že je to pravda jen částečně. Pokud se nesnažíme úlohu zformulovat aktivně a přímo jako testování hypotéz (spolu s jasnými kritérii), budeme samovolně směřovat k přidávání dalších parametrů do modelu tak, aby byl model nakalibrován a obhájen – nikoliv vyvrácen. Validace je skutečně postup, který můžeme chápat jako testování hypotézy. Bývá však nedostatečné, pokud je jejím důsledkem další kalibrace s přidáváním parametrů bez přehodnocení struktury modelu. V praxi modely navíc často nebývají vůbec validovány. U případových studií nebyla dostupná data pro validaci. Přínosem pojetí modelů jako hypotéz je, že není třeba doplňovat data pro vyvracení hypotéz, které byly již vyvráceny jednoduchým modelem za nedostatku dat. Je tak možno se soustředit na získání dat potřebných pro vyvrácení zbylých hypotéz.
Alternativní geologické modely
Důležitou součástí koncepčního distribuovaného modelu podzemní vody je jeho struktura – konkrétně geologická struktura, tedy geologický model. Alternativní geologické modely demonstrují význam geologické strukturní nejistoty modelu proudění podzemní vody.
Refsgaard et al. (2012) uvádí klasifikaci metodik pro hodnocení nejistot v modelování podzemní vody:
Klasifikace metodik pro hodnocení nejistot modelů podzemní vody
- Geologické struktury (geometrie v geologických modelech).
- Více geologických modelů (známý problém je, že zvolené koncepční modely nikdy nezahrnou celý prostor možných modelů)
- Ruční (geologické modely jsou vytvořeny ruční interpretací)
- Stochastická – umožňuje kombinovat subjektivní geologické znalosti a geostatistické analýzy – např. T‑PROGS (Carle 1999)
- Efektivní parametry modelu (např. po částech konstantní hodnoty uvnitř strukturních elementů)
- Analýza Monte Carlo
- Regresní analýza
- Lokální heterogenity parametrů modelu (nepopsaná variabilita hydraulických veličin uvnitř jednotlivých geologických strukturních elementů).
- Analýza Monte Carlo s vysokým rozlišením – představuje následující kroky:
- Generovat více náhodných sad modelových parametrů (představujících jednu či více vlastností prostředí) na jemné modelové mřížce;
- vyřešit standardní rovnice proudění a transportu a
- statisticky analyzovat výsledky modelu (predikce).
- Regresní analýza
- Momentová rovnice
Podle Refsgaarda et al. (2012, s. 48) je metodika více modelů uznávána jako nejslibnější strategie pro hodnocení projevů nejistoty struktury modelu (Beven 2002; Neuman a Wierenga 2003; Poeter a Anderson 2005; Refsgaard et al. 2006). Významnou slabostí tohoto přístupu je, že zvolené modely jsou jen malou podmnožinou možných geologických konceptualizací.
Refsgaard et al. (2012) dále ukazuje, že strukturně-geologická nejistota se projeví především, když model předpovídá stav systému za podmínek odlišných od těch, na které byl model kalibrován (obrázek 6): „Our results show that the geological models are relatively less important for flow modeling, if calibration against head and discharge data is performed, and if model predictions are confined (i) to the same types of variables as the data used for calibration, and (ii) to similar situations with respect to climate, groundwater abstractions, etc. In such case the inevitable (unknown) errors in the geological interpretations can often to a large extent be compensated by biased parameter values, so that the model predictions become of the same quality or slightly less than the goodness of the calibration results. However, the geological model becomes crucial in situations, where groundwater models are used for extrapolation beyond the calibration base, e.g., for transport predictions or for predictions of the effects of future changes in abstraction or climate, when only head and discharge data for the present pumping situation or climate are available for calibration. In such situations, the geological structure uncertainty may often be the dominant source of uncertainty.” (Refsgaard et al. 2012, s. 48)
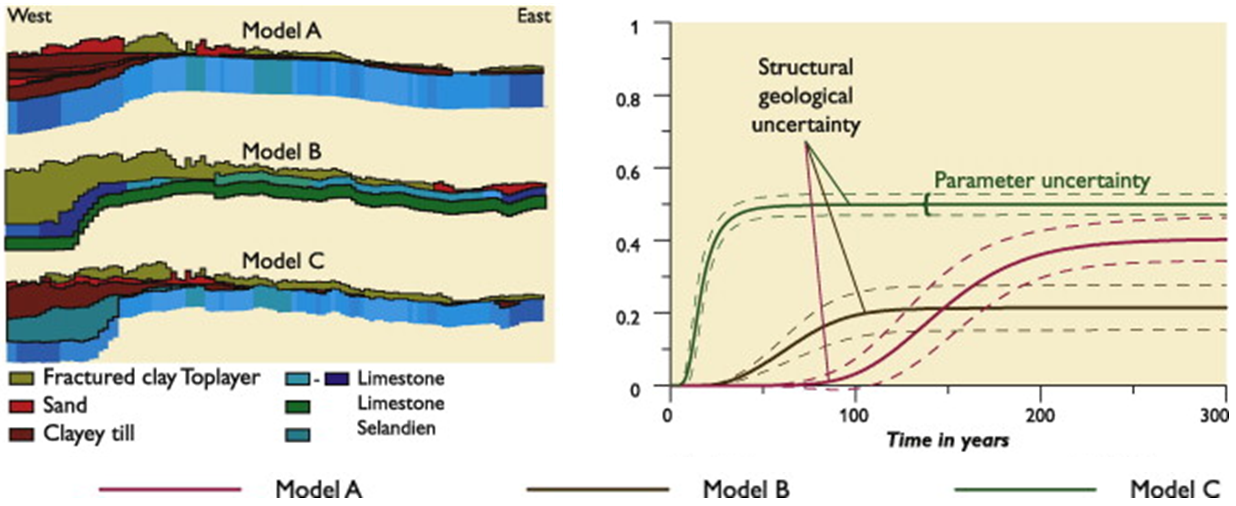 Obrázek 7: Citlivost predikcí modelu na alternativní geologické modely (Refsgaard et al. 2012) – výřez
Obrázek 7: Citlivost predikcí modelu na alternativní geologické modely (Refsgaard et al. 2012) – výřez
Princip ekvifinality
Formálnějším důvodem pro využití více modelů je princip ekvifinality (equifinality thesis; pojem z teorie systémů). Princip ekvifinality říká, že v systému existuje řada rozdílných cest vedoucích k dosažení požadovaného stavu. V kontextu modelování pak více modelů (lišících se strukturou či jen parametry) simulují srovnatelně chování systému. Modelové řešení daného problému proto není jednoznačné. Princip demonstruje, že často není možné nalézt správný model, což je typické postmoderní hledisko (Beven 1993). Průkopníkem vnímání principu ekvifinality v hydrologickém modelování je prof. Keith J. Beven (Beven 1993; 1996; 2001; 2009; 2010; Beven a Freer 2001). Rozsah výsledů sady ekvifinálních modelů charakterizuje její nejistotu (srov. tzv. envelope modeling).
Jednoduchost a komplexnost modelů podzemní vody
Současná hydrogeologie se propojuje s dalšími přírodovědnými obory. Hydrogeolog se tak setkává s fyzikálními, chemickými, mikrobiologickými a dalšími procesy a s jejich kombinací. Pokud se tyto procesy vzájemně ovlivňují, nazýváme je sdruženými procesy (coupled processes). Důkladná kvantifikace sdružených procesů není možná bez komplexních matematických modelů. Výsledky komplexních matematických modelů se někdy shodují s pozorováním, ač nejsou ve shodě s prvotní představou modeláře a nelze k nim dojít jednoduššími modely. To ukazuje jejich užitečnost a vede k používání stále komplexnějších a složitějších matematických modelů, obzvláště v oblasti vědy a výzkumu. Komplexní numerické modely jsou užitečným nástrojem pro porozumění a kvantifikaci přírodních jevů, zejména pak sdružených procesů. V praxi je však často účelnější použít jednodušší (např. analytické) modely. Je u nich jasnější vztah mezi předpoklady a výsledky modelu a jsou také vhodné pro testování hypotéz. Dobře umožňují získat cit pro simulované procesy a jsou pochopitelné např. pro řešitele komplexního projektu, kterému jsou výsledky určeny.
Komplexnost koncepčního modelu může vycházet z komplexnosti struktury modelu (nelineární) či parametrů (velký počet časově a prostorově proměnných parametrů) vyžadující numerické řešení. Jednoduchý model může být naopak lineární a celistvý (lumped) s analytickým řešením. Na rozdíl od pojetí předkládané práce Scheibe et al. (2015) spojuje komplexnost modelů podzemní vody s měřítkem – regionální modely jsou jednoduché a modely na molekulární úrovni jsou komplexní.
U komplexnějších modelů je možno dosáhnout shody s pozorováním kalibrací, čili manipulací s hodnotami parametrů díky vysokému počtu stupňů volnosti, zatímco u málo parametrizovaného modelu testujeme „čistou myšlenku“. Komplexnost modelu, která není podpořena daty ani neodpovídá pochopení probíhajícím procesům, bude mít pravděpodobně za důsledek nepřesný model (Hill 2006, s. 780). Přeparametrizovaný – tedy neadekvátně komplexní – model většinou nedává lepší předpovědi (obrázek 8).
Při studiu podzemní vody čelíme značné nejistotě. Podzemí je obtížně přístupné přímému pozorování a bývá navíc velice heterogenní. Tím se stává modelování často větší výzvou než v mnoha technických oborech. V terénním měřítku běžně hodnocených lokalit není v důsledku heterogenity prostředí dostupný dostatek adekvátních vstupních dat pro kalibraci komplexního modelu. Predikce nevhodně použitého modelu mohou být, zejména v dlouhém časovém měřítku, naprosto nespolehlivé.
Smysluplnost tradičního přístupu k modelování transportu (advekčně-disperzní rovnice bez difúze do bloků) zpochybňuje článek (Hadley a Newell 2014), který zdůrazňuje roli heterogenity prostředí a difúze do nepropustných bloků. Kontaminace se tak zpočátku může šířit velmi rychle (volná fáze, heterogenity s vysokou propustností), ale posléze je postup zastaven (difúze). To přináší nutnost uvažovat další neznámé (zastoupení jednotlivých domén, koeficient přestupu atd.). V článku je navrženo používat jednodušší nástroj Matrix Diffusion Toolkit (Farhat, et al. 2012), což je screeningový model (implementovaný v prostředí MS Excel) uvažující advekci a difúzi do málo propustných bloků. Z toho můžeme uvažovat, že pro porozumění chování kontaminace je třeba znát celou historii kontaminované lokality a zaměřit se na hodnocení a analýzy dostupných dat, nikoliv se spoléhat na prostorově distribuované modely.
Případové studie demonstrují, že jednoduchý model může dát odpověď, kterou není možno přímo dát numerickým modelem: dovolené čerpání (kap. 2.3.2) a bezpečná rychlost napouštění jezu (kap. 2.2).
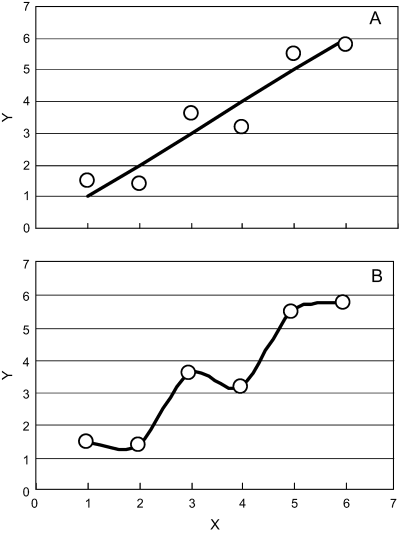 Obrázek 8: Schematický diagram – jednoduchý model (A) a komplexnější model (B). Zdroj: Hill (2006)
Obrázek 8: Schematický diagram – jednoduchý model (A) a komplexnější model (B). Zdroj: Hill (2006)
Dobrým zvykem v matematickém modelování je co nejjednodušším způsobem kvantifikovat přírodní procesy a postupně přidávat komplexnost. To ilustruje shrnutí vhodných a nevhodných přístupů k modelování (tabulka 6) a několik citátů: Modely podzemí vody by měly být „tak jednoduché, jak je to jen možné, ale nikoliv jednodušší“ 3) (Kraemer et al. 2000, s. 58). Simmons a Hunt (2012) označili takový přístup jako holistic parsimony. Poeticky se přílišnému zjednodušení říká kulová kráva (spherical cow), což je i součástí názvu dvou knih (Harte 1988; 2001). Příliš zjednodušující má v angličtině jednoslovné pojmenování: simplistic. V extrémním případě by bylo možno tuto tendenci označit za vulgarizaci.
„Pokud používáme modely v souladu s jejich cílem, měli bychom odolat volání sirény komplexnosti a sestavovat jednodušší a méně obsažné modely“4) (Hunt a Zheng 1999, s. 29). „Freyberg (1988) si všiml, že při cvičeních modelování, která vedl, bylo chování systému lépe předpovězeno jednoduššími a méně kalibrovanými modely než modely, které byly kalibrovány za použití velkého počtu parametrů, aby tak bylo dosaženo dobré shody s pozorováními (jev často nazývaný jako bodová kalibrace)“5) (Hunt et al. 2007, s. 254). Sbírka podobných citátů je uvedena samostatně.
Tabulka 6: Vhodné a nevhodné využití modelů podzemní vody podle citátů
| Vhodné využití modelů podzemní vody | Nevhodné využití modelů podzemní vody |
|---|---|
| Jednoduché (Occamova břitva6), princip jednoduchosti)7) | Příliš komplexní (avšak začít příliš jednoduchým je v pořádku) |
| Silný nástroj, který uspořádává myšlenky, tříbí úsudek a vybaví hydrogeologa teoreticky a vědecky podloženou intuicí | Cíl sám o sobě |
| Více koncepčních modelů | Příliš mnoho parametrů v jednom modelu |
| Zda se něco může stát (proof-of-concept) | Řešič problémů reálného světa |
| Testování hypotéz | Kvantitativní předpovědi (vhodné pokud jsou dostatečně podpořeny daty) |
| Počítačová podpora myšlení | Počítačová podpora předpovědí |
| Důležité jsou vzorce (patterns) chování, které jsou naznačeny čísly | Důležitá jsou čísla |
Bredehoeft (2006) doporučuje použití analytických modelů v případech, kdy jsou dostačující a uvádí příklad s čerpáním podzemní vody v blízkosti vodního toku.
Haitjema (2006) ukazuje užitečnost jednoduchých modelů podzemní vody (analytických řešení). Takové jednoduché výpočty jsou užitečné pro pochopení mechanismu probíhajících procesů spíše než pro získání kvantitativního řešení problému. Autor dále zdůrazňuje potřebu využívat analytická řešení při výuce matematického modelování, protože intuice získaná pomocí využívání analytických řešení často popírá prvotní intuici nezkušeného studenta.
Peeters (2015) klade modeláři na srdce, aby samostatně myslel, využíval zkušenosti z lokality a „neschovával se“ za dávno publikované postupy a hodnoty.
Wainwright a Mulligan (2013) ukazují na příkladech z různých oblastí environmentálního modelování pozorovanou komplexnost probíhajících procesů a možnost a účelnost využití jednoduchých modelů.
Přes tuto vehementní chválu jednoduchých modelů autor předkládané práce samozřejmě netvrdí, že jednoduché modely jsou vždy lepší. Na alternativní jednoduché modely (prototypy) má v ideálním případě navázat komplexnější model. Vždyť Engelhardt et al. (2014) srovnává modely s různým počtem parametrů pomocí informačních kritérií. Jako optimální modely se ukazují ty se střední komplexností (obrázek 9).
Adekvátním přístupem může být shromáždit data a ta pak zobrazit, statisticky zpracovat a interpretovat. Pro případ např. kontaminační hydrogeologie pak může být vhodné sestavit (0D) geochemický model a s jeho pomocí identifikovat klíčové řídicí procesy (např. aerobní biodegradace toluenu). Následně tyto procesy využít ve zjednodušené formě v modelu transportu v měřítku celé lokality (2D/3D).
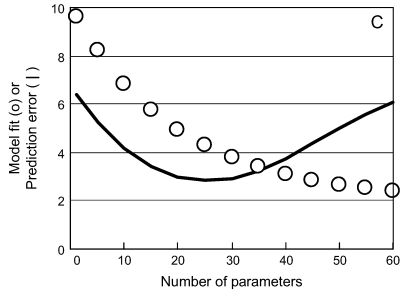 Obrázek 9: Schematický diagram ukazující kompromis mezi shodou modelu s pozorováním a přesností předpovědí s rostoucím počtem parametrů. Zdroj: Hill (2006)
Obrázek 9: Schematický diagram ukazující kompromis mezi shodou modelu s pozorováním a přesností předpovědí s rostoucím počtem parametrů. Zdroj: Hill (2006)
Vhodným přístupem je tzv. tiered approach (Lofts et al. 2019), kde je komplexnější model použit, jen pokud jednodušší pesimistický model nevyloučil hodnocené riziko (obrázek 10).
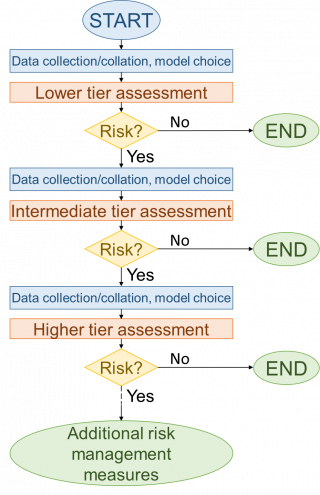 Obrázek 10: Generalised workflow for three tier exposure assessment framework (Lofts et al. 2019)
Obrázek 10: Generalised workflow for three tier exposure assessment framework (Lofts et al. 2019)
- Low tier simple worst case assessments using hand calculations
- Intermediate tier assessment using multiple environmental compartments
- Higher tier assessment using distributed model and complex processes
Alternativní jednoduché modely
Na zpracování matematického modelu v praxi zpravidla bývá omezený čas, ve kterém je možno sestavit komplexní numerický model. Jiný přístup může být ten, že je věnováno více času zpracovávání dat a promýšlení, jak systém funguje. Takové konkrétní představy je následně možné často kvantifikovat jednoduchými (např. analytickými) modely a testovat jimi alternativní koncepční modely (hypotézy).
Použití většího množství jednodušších modelů umožňuje zadávat hodnoty vstupních parametrů tak, aby odpovídaly cíli konkrétního dílčího modelu. Vhodně využité matematické modely pomáhají navrhnout, která data je třeba doplnit, abychom model omezili daty a zmenšili nejednoznačnost.
Alternativními jednoduchými modely se teoreticky zabývá opinion paper (Clark et al. 2011). Jeho autoři navrhují přístup více hypotéz, který však chápu jako software (sw) či framework, kde alternativní modely představují stejně či různě komplexní kvantifikace procesů.
Podle Haitjema (2015) adekvátní model dává požadované odpovědi a odpovídá finančním možnostem zadavatele. Podle něj je třeba přidávat komplexnost modelu, jen dokud se výsledky neustálí. Ekvifinální modely jsou tak modely lišící se jen různou komplexností.
Jednodušší modely je snadnější testovat (refutability), posoudit adekvátnost jejich struktury (transparency) a je u nich také snadnější vyhodnotit výsledky (Oreskes 2000).
Pokud alternativní koncepční modely vznikají nezávislým zjednodušováním komplexní reality, je možné je využít pro hodnocení strukturní nejistoty modelu. Uusitalo et al. (2015, s. 28) uvádí: „The system and model uncertainties can, to some extent, be addressed by using multiple models developed to describe the same domain. Simplifications, assumptions about dependencies between the variables, and various parameterizations are always made whenever a model is constructed. If these choices are made independently for each model, there is a possibility to use these separate models in structural uncertainty assessment.”
Jednoduchý model (např. kapitola Transport chlorovaných uhlovodíků – advekční a bilanční model) je jednodušší a proto průkaznější, v mnoha případech by však takový model neumožnil vyvrátit hypotézu, protože model musí být na straně bezpečnosti kvůli nekorektní kvantifikaci procesů. Pokud je však hypotéza zamítnuta, je toto zamítnutí průkaznější, protože u jednoduchého modelu je nižší pravděpodobnost, že obsahuje skrytou vadu či jinou „záludnost“. To se podobá statistickému usuzování, kdy při nastavení nízké hladiny významnosti (α) se často nepodaří hypotézu zamítnout. Přitom je vhodné využívat test s největší silou (1–β).
Využití více jednoduchých modelů má paralelu také v řízení projektů. Nejprve je třeba vytvořit počáteční návrh v různých variantách. Vybraný návrh je pak detailně rozpracován. Vágnější souvislost je s diverzifikací portfolia a radou, abychom nedávali všechny vejce do jednoho košíku.
Alternativní jednoduché modely je tak možno nadneseně chápat jako prototypy a to tzv. horizontal (předběžná kvantifikace různých hypotéz či způsobů řešení), throwaway (testování hypotéz) či incremental (např. části lokality jsou řešeny různými přístupy) – Software prototyping.
Ve statistice je samozřejmým přístupem provádět nejprve průzkumovou analýzu dat (exploratory data analysis), a s její pomocí formulovat více hypotéz (modelů) od nejjednodušších ke složitějším. Předkládaná práce má proto téma, které je na jedné straně banální, avšak v hydrogeologii není zdaleka tak samozřejmé jako právě ve statistice. Fyzikální podstata problému totiž vede modeláře samovolně k využití distribuovaných modelů, které využívají matematicky korektní formulaci hydrogeologické úlohy – a to i když to není nutné či adekvátní.
Jednoduché alternativní modely jsou obranou proti chybám v myšlení a argumentaci (fallacies, biases): např. konfirmační zkreslení (confirmation bias) – (Bond 2015). To potvrzuje Peeters (2017, s. 665): „We often have the tendency to settle upon a conceptual model early on in a project and get caught in confirmation bias. … One practical way to do this is, when creating a conceptual or numerical model, is to consider at least one alternative for each choice and assumption and capturing this in a modeling log.“
Ekvifinalita – vymezení vůči dostupným publikacím
V dostupné literatuře se často diskutuje účelnost jednoduchých modelů či princip ekvifinality, ale nikoliv obé zároveň. Hellebrand et al. (2011) zmiňuje princip ekvifinality v kontextu hydrologických modelů. Srovnává málo parametrizované hydrologické modely, které kvantifikují jednotlivé mechanismy odtoku. Selroos et al. (2002) simuloval proudění podzemní vody a transport rozpuštěných látek v puklinovém prostředí za pomoci tří přístupů (stochastické kontinuum, síť diskrétních puklin a síť 1D potrubí). V jiné práci (Singh et al. 2010) byly alternativní koncepční modely realizovány sadami parametrů téhož modelu. Další (Elshall a Tsai 2014; Harrar et al. 2003; Neuman a Wierenga 2003; Nilsson et al. 2007; Passadore et al. 2012; Pirot et al. 2015; Rojas et al. 2010; Seifert et al. 2008; Ye et al. 2010) použili alternativní koncepční modely (geologické, výpočet evapotranspirace atd.), které však byly implementovány v MODFLOW či v podobných programech jako třeba MIKE SHE (Seifert et al. 2012; Butts et al. 2004; Troldborg et al. 2007).
Gupta et al. (2012) se zaměřil na strukturální adekvátnost a možnost jejího hodnocení. Ta podle něj pro modely podzemní vody odpovídá 3D hydrostratigrafii, což je z pohledu autora předkládané práce pojetí zúžené na komplexnější 2D/3D modely.
Adams a Younger (2001) se zabývali různými způsoby přístupu k modelování zatápění dolů. Různé přístupy jsou uvedeny podle vhodnosti od detailního k regionálnímu měřítku:
- průlinový model proudění kombinovaný s explicitně definovanou sítí důlních děl;
- semidistribuovaný model, kde jsou jednoduše analyticky vyjádřené nádrže důlní vody propojeny analyticky modelovaným potrubím a
- model ekvivalentního kontinua (MODFLOW).
Předkládaná práce se nezabývá jen ekvifinálními modely, ale obecněji principiálně odlišnými koncepčními modely (multiple model ensemble).
Formulace zvoleného přístupu
Studie zmiňující princip ekvifinality v podstatě vždy využívají sadu parametrů pro jeden model. To je praktické v případě hydrologických modelů, kde jsou dostupné dlouhé časové řady významných veličin (průtok ve vodním toku je soustředěný – integrovaný – odtok z celého dílčího povodí) a mnohé parametry jsou známy se značnou přesností (např. terén). V případě podzemní vody může být epistemologická nejistota větší. Neznáme přesně směr proudění a preferenční cesty; někdy neznáme všechna ohniska kontaminace, a zda se kontaminace šíří horninovým prostředím či například umělým drénem apod. U povrchových vod alespoň vždy víme, že vodní tok existuje a kde se nachází. V případě řešení praktických hydrogeologických úloh často nemáme dostupná dostatečná data (o časových řadách ani nemluvě).
Proto jde předkládaná práce v aplikaci principu ekvifinality ještě dál a nevytváří alternativní sady parametrů (varianty, scénáře) ani alternativní geologické modely, ale jednoduché alternativní modely, které simulují jiné procesy, používají jinou metodu či představují odlišné koncepční přístupy (jsou principiálně odlišné). Případové studie často vychází z nedostatečných vstupních dat (a tedy i informací a znalostí o lokalitě – tak i dále) a není účelné a často ani možné modely kvantitativně srovnávat (viz průměrování modelů jako např. GLUE). Modely tak nejsou kalibrované ani validované. V některých případových studiích se neuplatňuje princip ekvifinality, protože modely se doplňují (např. kapitola Kombinace principiálně odlišných modelů – model délky kontaminačního mraku a dovoleného čerpání).
Schéma na obrázku 11 představuje dvojnásobnou transformaci dat ve znalosti. Jednoduchý model (šipky nahoře a dole) umožňuje tuto transformaci zjednodušit mj. tím, že nezavádí do koncepčního modelu nepodložené předpoklady (neznámé parametry), jejichž vliv na výsledek by bylo třeba vyhodnotit. Je srozumitelné, z jakých předpokladů vycházejí. Strategii je možno nadneseně vyjádřit takto: „Je lepší vytvářet jednoduché modely nad měřenými daty než komplexní modely nad vymyšlenými daty.“
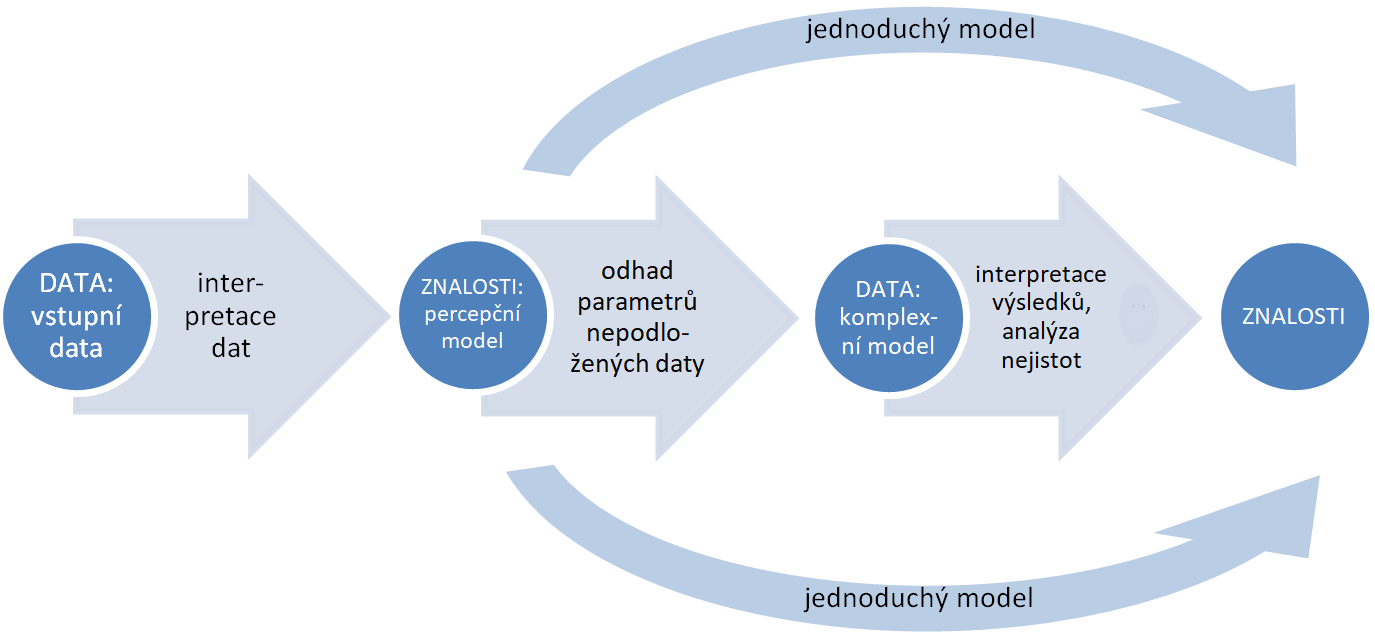 Obrázek 11: Data a znalosti – jednoduchý model má o jednu transformaci méně
Obrázek 11: Data a znalosti – jednoduchý model má o jednu transformaci méně
Alternativní jednoduché modely mohou být účelně využívány různým způsobem. Jednoduchost tvorby modelů dává větší prostor pro využití modelu rozmanitým způsobem, aby tak byl vhodným nástrojem pro podporu rozhodování, a to i v případě nedostatku dat. Předkládaná práce navrhuje klasifikaci využití modelů se zaměřením na jednoduché modely sestavené při nedostatku dat. Je to tedy souhrn otázek, které může zadavatel klást (zpracovateli) modelu:
- Interpretační model – Porozumění probíhajícím procesům / tvorba koncepčního modelu – pomocí modelu, který odpovídá měřením prokázat, že naše porozumění procesům odpovídá měřeným výsledkům a případně, že data jsou vnitřně konzistentní.
- Testování hypotéz – Příklad: Ani nejodvážnější fyzikálně možná kombinace parametrů modelu není schopna generovat výsledek, který odpovídá pozorování – proto je struktura modelu chybná, a tedy procesy, na kterých je model založen, nejsou dostatečné pro simulování skutečného chování systému. Případ využití tohoto přístupu je v kapitole Ekvifinalita – interakce povrchové a podzemní vody a kapitole Transport chlorovaných uhlovodíků – advekční a bilanční model.
- Vztah modelu a události či jevu
- „Proof of concept“ – Měřené či alespoň fyzikálně možné hodnoty modelu jsou schopny popsat vzorec (pattern) chování systému. Struktura modelu tak může být správná a simulované procesy mohou být schopny vysvětlit chování systému. Například: Stratifikaci jezera je možno vysvětlit působením větru a teploty, jež ovlivňuje hustotu vody.
- „Inverzní model“ – zjišťování parametrů modelu, které odpovídají meznímu požadovanému (nežádoucímu) stavu (např. nárůst látkového toku kontaminace v recipientu nad stanovenou hodnotu; výtopa chráněného území apod.). Výsledkem je parametr (například hydraulická vodivost), který je třeba ověřit podrobným průzkumem. Přístup je využit v kapitole Transport ropných uhlovodíků.
- Hodnocení vlivu očekávaných změn:
- Analýza citlivosti – ukazuje, které parametry výrazně ovlivňují výsledky modelu.
- Scénáře – typové varianty budoucího vývoje (projection, what-if simulation, „co se stane když“) – pojem: Beven a Young (2013) a kapitola Matematické modely podzemní vody.
- Předpovědi budoucnosti – pojmy: Beven a Young (2013) a kapitola Matematické modely podzemní vody.:
- Ex-post forecasting (méně vhodně: prediction) – předpokládáme konkrétní časový vývoj parametrů modelu. Příkladem je model v kapitole Srovnání jednoduchého a komplexního modelu – ovlivnění podzemních vod jezem. Při nejistotě vstupních dat je možné použít variantní výpočty (scénáře): např. optimistický, pesimistický či realistický.
- Ex-ante forecasting – model počítá vývoj celého systému.
- Analýza nejistoty – Jak spolehlivé jsou výsledky modelu.
- Analýza citlivosti – Jaká data jsou pro hodnověrnost modelu nejdůležitější? Parametry s vysokou citlivostí totiž výrazně ovlivňují výsledky modelu, a proto je třeba určit je s maximální přesností.
- Neparametrický výpočet – Např. porovnání doby doběhu radionuklidů do recipientu pro různé lokality jaderného úložiště při stejné hodnotě hydraulické vodivosti pro všechny lokality. Je tak hodnocen vliv geometrie problému, nikoliv jeho parametrů. Jedná se o relativní srovnání lokalit.
Takováto klasifikace strategií modelování či formulování zadání, na které může model odpovědět, nebyla v literatuře nalezena – kromě neúplné klasifikace (Bredehoeft 2005). Uvedená klasifikace ukazuje, že výsledkem modelů nemusejí být předpovědi týkající se budoucnosti, byť by byl zprvu zadavatelem požadavek právě tak formulován.
Alternativní modely jsou v praxi používány, ačkoli se v tomto kontextu nemluví o ekvifinalitě. Toto téma je však natolik závažné, že stojí za hlubší rozbor, a je tak přínosem k debatě ve vědeckých časopisech, jež v současnosti intenzivně probíhá. Níže představené případové studie originálním způsobem demonstrují výše uvedené principy. Nepředstavují schematický přístup, ke kterému vede řešení problematiky za pomoci existujících softwarových balíků pro modelování podzemní vody, ale nespoutané přemýšlení, které je ve shodě se současnou filosofií vědy – epistemologickým anarchismem (Feyerabend 1975; 2001).
Případové studie
Případové studie – kapitola byla vyčleněna na samostatnou stránku 
Shrnutí a závěr
Podzemí je obtížně přístupné přímému pozorování a bývá navíc velice heterogenní. Proto při studiu podzemní vody čelíme značné nejistotě. Práce reaguje na nejistotu ve výsledcích modelů podzemní vody. V práci je představeno shrnutí existujících klasifikací nejistot (zejm. koncepčního modelu). Je zde definována epistemologická nejistota a její projevy: nejistota koncepčního modelu a nejistota struktury modelu.
Pro vypořádání se s takovou nejistotou je v práci obhajována a využita strategie více jednoduchých modelů. Ta nespočívá ve vytváření alternativních sad parametrů (varianty, scénáře) ani alternativních geologických modelů, ale ve využití jednoduchých alternativních modelů, které simulují jiné procesy, používají jinou metodu či představují odlišné koncepční přístupy (jsou principiálně odlišné). Tyto jednoduché modely mohou být formulovány jako testování hypotéz a jednoznačně snižovat nejistotu porozumění fungování studovaného systému. Zvolená strategie podle klasifikace Uusitalo et al. (2015) přibližně odpovídá kombinaci přístupů „emulace modelu“ a „více modelů“ a také odpovídá tzv. „multiple model ensemble”. Podle Refsgaarda et al. (2007) odpovídá kategorii „simulace více modely – modely s odlišnou strukturou“. Využití modelů pro testování hypotéz je spolu s dalšími uveden v navržené klasifikaci využití modelů (interpretační model, testování hypotéz, proof of concept, hodnocení vlivu očekávaných změn, předpovědi budoucnosti, analýza nejistoty, analýza citlivosti, neparametrický výpočet). V práci je diskutováno použití principu ekvifinality a tohoto pojmu v oblasti modelování podzemní vody.
Strategie více jednoduchých modelů je demonstrována na případových studiích, které vycházejí z malého množství adekvátních vstupních dat. Jedna úloha je řešena více modely, které jsou založeny na různých přístupech a předpokladech. Prezentované případové studie srovnávají jednoduché a komplexní modely, testují alternativní hypotézy sadou jednoduchých modelů či představují alternativní prediktivní modely. Obhajitelnost modelů v případových studiích byla semikvantitativně vyhodnocena podle metodiky Refsgaarda et al. (2006).
Bredehoeft (2005) uvádí, že mnozí autoři navrhují využití alternativních koncepčních modelů, ale že nikdy nezaznamenal uskutečnění tohoto přístupu v praxi, protože modeláři pracují s jedním koncepčním modelem, který mění až v případě, kdy jej není možné nakalibrovat. Předkládaná práce naopak ukazuje, jak je možno uplatnit alternativní koncepční modely v praxi – totiž používat (alespoň v první fázi) více jednoduchých modelů.
Doufám, že tato práce bude inspirací pro dobrou praxi v modelování podzemní vody – abychom více přemýšleli a méně počítali; neřídili se šablonami, ale vytvářeli modely, jež jsou účelné, i kdyby se nebylo třeba dobrat až ke komplexnímu modelu. Tedy: ne data do modelu, ale model nad daty.
Použitá literatura
ADAMS, R. a P.L. YOUNGER, 2001. A strategy for modeling ground water rebound in abandoned deep mine systems. Ground Water. 39(2), 249–261. 10.1111/j.1745-6584.2001.tb02306.x
BEVEN, K., 1996. Equifinality and uncertainty in geomorphological modelling. In: B. L. RHOADS a C. E. THORN, ed. 27th Binghamton Symposium in Geomorphology: Scientific Nature of Geomorphology. Chichester: John Wiley & Sons Ltd, s. 289–313. ISBN 0-471-96811-0.
BEVEN, Keith, 1993. Prophecy, reality and uncertainty in distributed hydrological modelling. Advances in Water Resources. 16(1), 41–51. ISSN 0309-1708. 10.1016/0309-1708(93)90028-E
BEVEN, Keith, 2002. Towards an alternative blueprint for a physically based digitally simulated hydrologic response modelling system. Hydrological Processes. 16(2), 189–206. ISSN 1099-1085. 10.1002/hyp.343
BEVEN, Keith, 2006. A manifesto for the equifinality thesis. Journal of Hydrology. 320(1–2), 18–36. ISSN 0022-1694. 10.1016/j.jhydrol.2005.07.007
BEVEN, Keith, 2012. Rainfall-runoff modelling: the primer. Second Edition. Chichester, UK: John Wiley & Sons, Ltd. ISBN 978-1-119-95100-1. 10.1002/9781119951001
BEVEN, Keith a Jim FREER, 2001. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. Journal of Hydrology. 249(1–4), 11–29. ISSN 0022-1694. 10.1016/S0022-1694(01)00421-8
BEVEN, Keith J., 2001. Rainfall-runoff modelling: the primer. Chichester: Wiley. ISBN 9780470866719.
BEVEN, Keith J., 2009. Environmental modelling: An uncertain future?: An introduction to techniques for uncertainty estimation in environmental prediction. London; New York: Routledge. ISBN 978-0-415-46302-7.
BEVEN, Keith J., 2010. Preferential flows and travel time distributions: defining adequate hypothesis tests for hydrological process models. Hydrological Processes. 24(12), 1537–1547. ISSN 0885-6087, 1099-1085. 10.1002/hyp.7718
BEVEN, Keith a Ida WESTERBERG, 2011. On red herrings and real herrings: disinformation and information in hydrological inference. Hydrological Processes. 25(10), 1676–1680. ISSN 1099–1085. 10.1002/hyp.7963
BEVEN, Keith a Peter YOUNG, 2013. A guide to good practice in modeling semantics for authors and referees. Water Resources Research. 49(8), 5092–5098. ISSN 1944-7973. 10.1002/wrcr.20393
BOND, Clare E., 2015. Uncertainty in structural interpretation: Lessons to be learnt. Journal of Structural Geology. 74, 185–200. ISSN 0191-8141. 10.1016/j.jsg.2015.03.003
BREDEHOEFT, J., 2006. On modeling philosophies. Ground Water. 44(4), 496–499. ISSN 0017-467X. 10.1111/j.1745-6584.2006.00232.x
BREDEHOEFT, John, 2005. The conceptualization model problem—surprise. Hydrogeology Journal. 13(1), 37–46. 10.1007/s10040-004-0430-5
BREUER, L., J. A. HUISMAN, P. WILLEMS, H. BORMANN, A. BRONSTERT, B. F. W. CROKE, H. G. FREDE, T. GRÄFF, L. HUBRECHTS, A. J. JAKEMAN, G. KITE, J. LANINI, G. LEAVESLEY, D. P. LETTENMAIER, G. LINDSTRÖM, J. SEIBERT, M. SIVAPALAN a N. R. VINEY, 2009. Assessing the impact of land use change on hydrology by ensemble modeling (LUCHEM). I: Model intercomparison with current land use. Advances in Water Resources. 32(2), 129–146. ISSN 0309-1708. 10.1016/j.advwatres.2008.10.003
BROWN, James D, 2004. Knowledge, uncertainty and physical geography: towards the development of methodologies for questioning belief. Transactions of the Institute of British Geographers. 29(3), 367–381. ISSN 1475–5661. 10.1111/j.0020-2754.2004.00342.x
BROWN, J.D., G.B. HEUVELINK a J.C. REFSGAARD, 2005. An integrated methodology for recording uncertainties about environmental data. Water Science and Technology. 52(6), 153–160.
BUTTS, Michael B., Jeffrey T. PAYNE, Michael KRISTENSEN a Henrik MADSEN, 2004. An evaluation of the impact of model structure on hydrological modelling uncertainty for streamflow simulation. Journal of Hydrology. 298(1–4), The Distributed Model Intercomparison Project (DMIP), 242–266. ISSN 0022-1694. 10.1016/j.jhydrol.2004.03.042
CLARK, Martyn P., Dmitri KAVETSKI a Fabrizio FENICIA, 2011. Pursuing the method of multiple working hypotheses for hydrological modeling. Water Resources Research. 47(9), W09301. ISSN 1944-7973. 10.1029/2010WR009827
CLARK, Martyn P., Bart NIJSSEN, Jessica D. LUNDQUIST, Dmitri KAVETSKI, David E. RUPP, Ross A. WOODS, Jim E. FREER, Ethan D. GUTMANN, Andrew W. WOOD, Levi D. BREKKE, Jeffrey R. ARNOLD, David J. GOCHIS a Roy M. RASMUSSEN, 2015a. A unified approach for process-based hydrologic modeling: 1. Modeling concept: A unified approach for process-based hydrologic modeling. Water Resources Research. 51(4), 2498–2514. ISSN 00431397. 10.1002/2015WR017198
CLARK, Martyn P., Bart NIJSSEN, Jessica D. LUNDQUIST, Dmitri KAVETSKI, David E. RUPP, Ross A. WOODS, Jim E. FREER, Ethan D. GUTMANN, Andrew W. WOOD, David J. GOCHIS, Roy M. RASMUSSEN, David G. TARBOTON, Vinod MAHAT, Gerald N. FLERCHINGER a Danny G. MARKS, 2015b. A unified approach for process-based hydrologic modeling: 2. Model implementation and case studies: A unified approach for process-based hydrologic modeling. Water Resources Research. 51(4), 2515–2542. ISSN 00431397. 10.1002/2015WR017200
COULIBALY, Paulin, François ANCTIL, Ramon ARAVENA a Bernard BOBÉE, 2001. Artificial neural network modeling of water table depth fluctuations. Water Resources Research. 37(4), 885–896. ISSN 00431397. 10.1029/2000WR900368
ELSHALL, Ahmed S. a Frank T. C. TSAI, 2014. Constructive epistemic modeling of groundwater flow with geological structure and boundary condition uncertainty under the Bayesian paradigm. Journal of Hydrology. 517, 105–119. ISSN 0022-1694. 10.1016/j.jhydrol.2014.05.027
ENGELHARDT, I., J.g. DE AGUINAGA, H. MIKAT, C. SCHÜTH a R. LIEDL, 2014. Complexity vs. simplicity: Groundwater model ranking using information criteria. Groundwater. 52(4), 573–583. ISSN 1745-6584. 10.1111/gwat.12080
FARHAT, S.K., C.J. NEWELL, T.C. SALE, D.S. DANDY, J.J. WAHLBERG, M.A. SEYEDABBASI, J.M. MCDADE a N.T. MAHLER, 2012. Matrix Diffusion Toolkit. Houston, Texas: Developed for the Environmental Security Technology Certification Program (ESTCP) by GSI Environmental Inc. https://www.gsienv.com/product/matrix-diffusion-toolkit/
FARRELL, D.M., B.S. MINSKER, D. TCHENG, D. SEARSMITH, J. BOHN a D. BECKMAN, 2007. Data mining to improve management and reduce costs of environmental remediation. Journal of Hydroinformatics. 9(2), 107–121.
FERRÉ, Ty P.A., 2017. Revisiting the relationship between data, models, and decision-making. Groundwater. 55(5), 604–614. ISSN 1745-6584. 10.1111/gwat.12574
FEYERABEND, Paul, 1975. Against method: outline of an anarchistic theory of knowledge. London: Atlantic Highlands: NLB; Humanities Press. ISBN 0-902308-91-2.
FEYERABEND, Paul, 2001. Rozprava proti metodě. Přel. Jiří FIALA. Praha: Aurora. ISBN 80-7299-047-0.
FREYBERG, David L., 1988. An exercise in ground-water model calibration and prediction. Ground Water. 26(3), 350–360. 10.1111/j.1745-6584.1988.tb00399.x
GUPTA, Hoshin V., Martyn P. CLARK, Jasper A. VRUGT, Gab ABRAMOWITZ a Ming YE, 2012. Towards a comprehensive assessment of model structural adequacy. Water Resources Research. 48(8), W08301. 10.1029/2011WR011044
HADLEY, Paul W. a Charles NEWELL, 2014. The new potential for understanding groundwater contaminant transport. Groundwater. 52(2), 174–186. ISSN 1745-6584. 10.1111/gwat.12135
HAITJEMA, Henk, 2006. The role of hand calculations in ground water flow modeling. Ground Water. 44(6), 786–791. ISSN 0017-467X. 10.1111/j.1745-6584.2006.00189.x
HAITJEMA, Henk M., 2015. The cost of modeling. Groundwater. 53(2), 179. ISSN 1745-6584. 10.1111/gwat.12321
HARRAR, William G., Torben Obel SONNENBORG a Hans Jørgen HENRIKSEN, 2003. Capture zone, travel time, and solute-transport predictions using inverse modeling and different geological models. Hydrogeology Journal. 11(5), 536–548. ISSN 1431-2174, 1435-0157. 10.1007/s10040-003-0276-2
HARTE, John, 1988. Consider a spherical cow: a course in environmental problem solving. Nachdr. Sausalito, Calif: Univ. Science Books. ISBN 978-0-935702-58-3. https://uscibooks.aip.org/authors/john-harte/
HARTE, John, 2001. Consider a cylindrical cow: more adventures in environmental problem solving. Sausalito, Calif: University Science Books. ISBN 978-1-891389-17-7. https://uscibooks.aip.org/authors/john-harte/
HELLEBRAND, Hugo, Christoph MÜLLER, Patrick MATGEN, Fabrizio FENICIA a Huub SAVENIJE, 2011. A process proof test for model concepts: Modelling the meso-scale. Physics and Chemistry of the Earth, Parts A/B/C. 36(1–4), 42–53. ISSN 1474-7065. 10.1016/j.pce.2010.07.019
HILL, Mary C., 2006. The practical use of simplicity in developing ground water models. Ground Water. 44(6), 775–781. 10.1111/j.1745-6584.2006.00227.x
HILL, Mary C. a Claire R. TIEDEMAN, 2007. Effective groundwater model calibration: with analysis of data, sensitivities, predictions, and uncertainty. Hoboken N.J.: Wiley-Interscience. ISBN 978-0-471-77636-9.
HUNT, R. a C. ZHENG, 1999. Debating complexity in modeling. Eos, Transactions, American Geophysical Union. 80(3), 29. ISSN 0096-3941. 10.1029/99EO00025
HUNT, Randall J., John DOHERTY a Matthew J. TONKIN, 2007. Are models too simple? Arguments for increased parameterization. Ground Water. 45(3), 254–262. 10.1111/j.1745-6584.2007.00316.x
CHAMBERLIN, Thomas Chrowder, 1890. The method of multiple working hypotheses. Science. 15(366), 92–96.
KRAEMER, S., H. HAITJEMA a V. KELSON, 2000. Working with WhAEM2000: Source water assessment for a glacial outwash wellfield, Vincennes, Indiana. EPA/600/R-00/022. Washington: Office of Research and Development, US Environmental Protection Agency.
KREŠIĆ, Neven a Alex MIKSZEWSKI, 2012. Hydrogeological conceptual site models: data analysis and visualization. Boca Raton, FL: CRC Press. ISBN Print: 978-1-4398-5222-4 eBook: 978-1-4398-5228-6. https://www.routledge.com/Hydrogeological-Conceptual-Site-Models-Data-Analysis-and-Visualization/Kresic-Mikszewski/p/book/9781439852224#
KREYE, Melanie E., Yee Mey GOH a Linda B. NEWNES, 2011. Manifestation of uncertainty – a classification. Proceedings of the 18th International Conference on Engineering Design (ICED 11): Impacting Society Through Engineering Design, Vol 6: Design Information and Knowledge. 6, 96–107. ISSN 2220-4334.
KUHN, Thomas S., 1970. The structure of scientific revolutions. Second Edition, enlarged. USA: University of Chicago Press. International encyclopedia of unified science. Foundations of the unity of science. ISBN 0-226-45803-2.
KUHN, Thomas S., 2008. Struktura vědeckých revolucí. 1. vyd. Přel. Tomáš JENÍČEK. Praha: OIKOYMENH. Knihovna novověké tradice a současnosti, Sv. 64. ISBN 978-80-86005-54-6.
LITAOR, M. Iggy, H. BRIELMANN, O. REICHMANN a M. SHENKER, 2010. Hydrochemical analysis of groundwater using a tree-based model. Journal of Hydrology. 387(3–4), 273–282. ISSN 0022-1694. 10.1016/j.jhydrol.2010.04.017
LOFTS, Stephen, Joris QUIK a Sam HARRISON, 2019. Workflow for a tiered exposure assessment. NanoFASE [Webová stránka evropského výzkumného projektu]. http://nanofase.eu/show/workflow-for-a-tiered-exposure-assessment_1962/
MAHMOUD, Mohammed, Yuqiong LIU, Holly HARTMANN, Steven STEWART, Thorsten WAGENER, Darius SEMMENS, Robert STEWART, Hoshin GUPTA, Damian DOMINGUEZ, Francina DOMINGUEZ, David HULSE, Rebecca LETCHER, Brenda RASHLEIGH, Court SMITH, Roger STREET, Jenifer TICEHURST, Mark TWERY, Hedwig VAN DELDEN, Ruth WALDICK, Denis WHITE a Larry WINTER, 2009. A formal framework for scenario development in support of environmental decision-making. Environmental Modelling & Software. 24(7), 798–808. ISSN 1364-8152. 10.1016/j.envsoft.2008.11.010
MANDEL, John, 1984. The Statistical Analysis of Experimental Data. New York: Dover Publications. ISBN 978-0-486-64666-4.
MARÇAIS, Jean a Jean-Raynald DE DREUZY, 2017. Prospective interest of deep learning for hydrological inference. Groundwater. 55(5), 688–692. ISSN 1745-6584. 10.1111/gwat.12557
MICHAEL, William J., Barbara S. MINSKER, David TCHENG, Albert J. VALOCCHI a John J. QUINN, 2005. Integrating data sources to improve hydraulic head predictions: A hierarchical machine learning approach. Water Resources Research. 41(3), 14 s. 10.1029/2003WR002802
NEUMAN, S. P. a P. J. WIERENGA, 2003. A comprehensive strategy of hydrogeologic modeling and uncertainty analysis for nuclear facilities and sites. NUREG/CR-6805. Tucson: University of Arizona. https://www.nrc.gov/reading-rm/doc-collections/nuregs/contract/cr6805/index.html
NILSSON, B., A. L. HOJBERG, J. C. REFSGAARD a L. TROLDBORG, 2007. Uncertainty in geological and hydrogeological data. Hydrology and Earth System Sciences. 11(5), 1551–1561. ISSN 1027-5606.
OCKAM, Guilielmus, 1495. Quaestiones et decisiones in quattuor libros Sententiarum Petri Lombardi: Centilogium theologicum. Lyon: Johannes Trechsel.
ORESKES, Naomi, 2000. Why believe a computer? Models, measures, and meaning in the natural world. In: Jill SCHNEIDERMAN, ed. The earth around us: Maintaining a livable planet. New York: W.H. Freeman, s. 70–82. ISBN 978-1-4668-1443-1.
PASSADORE, Giulia, Martina MONEGO, Lorenzo ALTISSIMO, Andrea SOTTANI, Mario PUTTI a Andrea RINALDO, 2012. Alternative conceptual models and the robustness of groundwater management scenarios in the multi-aquifer system of the Central Veneto Basin, Italy. Hydrogeology Journal. 20(3), 419–433. ISSN 1431-2174, 1435-0157. 10.1007/s10040-011-0818-y
PEETERS, Luk J. M., 2015. Editor’s Message: Stand on the shoulders of giants, don’t hide behind them. Hydrogeology Journal. 23(3), 421–422. ISSN 1431-2174, 1435-0157. 10.1007/s10040-015-1247-0
PEETERS, Luk J. M., 2017. Assumption hunting in groundwater modeling: find assumptions before they find you. Groundwater. 55(5), 665–669. ISSN 1745-6584. 10.1111/gwat.12565
PIROT, Guillaume, Philippe RENARD, Emanuel HUBER, Julien STRAUBHAAR a Peter HUGGENBERGER, 2015. Influence of conceptual model uncertainty on contaminant transport forecasting in braided river aquifers. Journal of Hydrology. 531, Part 1, Groundwater flow and transport in aquifers: Insights from modeling and characterization at the field scale, 124–141. ISSN 0022-1694. 10.1016/j.jhydrol.2015.07.036
POETER, Eileen, 2007. All models are wrong, how do we know which are useful? Ground Water. 45(4), 390–391. ISSN 1745-6584. 10.1111/j.1745-6584.2007.00350.x
POETER, Eileen a David ANDERSON, 2005. Multimodel ranking and inference in ground water modeling. Ground Water. 43(4), 597–605. ISSN 1745-6584. 10.1111/j.1745-6584.2005.0061.x
POPPER, Karl, 1997. Logika vědeckého bádání. 1. vyd. Přel. Jiří FIALA. Praha: OIKOYMENH. Oikúmené. ISBN 978-80-86005-45-4.
RAPANTOVÁ, Nad’a, Światosław KRZESZOWSKI, Arnošt GRMELA a Christian WOLKERSDORFER, 2012. Quantitative assessment of mine water sources based on the general mixing equation and multivariate statistics. Mine Water and the Environment. 31(4), 252–265. ISSN 1025-9112, 1616-1068. 10.1007/s10230-012-0192-6
RAZAVI, Saman, Bryan A. TOLSON a Donald H. BURN, 2012. Review of surrogate modeling in water resources. Water Resources Research. 48(7). ISSN 1944-7973. 10.1029/2011WR011527
REFSGAARD, Jens Christian a Hans Jørgen HENRIKSEN, 2004. Modelling guidelines – terminology and guiding principles. Advances in Water Resources. 27(1), 71–82. ISSN 0309-1708. 10.1016/j.advwatres.2003.08.006
REFSGAARD, Jens Christian, Steen CHRISTENSEN, Torben O. SONNENBORG, Dorte SEIFERT, Anker Lajer HØJBERG a Lars TROLDBORG, 2012. Review of strategies for handling geological uncertainty in groundwater flow and transport modeling. Advances in Water Resources. 36, Special Issue on Uncertainty Quantification and Risk Assessment, 36–50. ISSN 0309-1708. 10.1016/j.advwatres.2011.04.006
REFSGAARD, Jens Christian, Jeroen P. VAN DER SLUIJS, James BROWN a Peter VAN DER KEUR, 2006. A framework for dealing with uncertainty due to model structure error. Advances in Water Resources. 29(11), 1586–1597. ISSN 0309-1708. 10.1016/j.advwatres.2005.11.013
REFSGAARD, Jens Christian, Jeroen P. VAN DER SLUIJS, Anker Lajer HØJBERG a Peter A. VANROLLEGHEM, 2007. Uncertainty in the environmental modelling process – A framework and guidance. Environmental Modelling & Software. 22(11), 1543–1556. ISSN 1364-8152. 10.1016/j.envsoft.2007.02.004
ROACH, Jesse a Vince TIDWELL, 2009. A compartmental-spatial system dynamics approach to ground water modeling. Ground Water. 47(5), 686–698. ISSN 0017-467X. 10.1111/j.1745-6584.2009.00580.x
ROJAS, Rodrigo, Samalie KAHUNDE, Luk PEETERS, Okke BATELAAN, Luc FEYEN a Alain DASSARGUES, 2010. Application of a multimodel approach to account for conceptual model and scenario uncertainties in groundwater modelling. Journal of Hydrology. 394(3–4), 416–435. ISSN 0022-1694. 10.1016/j.jhydrol.2010.09.016
SAVENIJE, Hubert H. G., 2001. Equifinality, a blessing in disguise? Hydrological Processes. 15(14), 2835–2838. ISSN 1099-1085. 10.1002/hyp.494
SEIFERT, Dorte, Torben O. SONNENBORG, Jens Christian REFSGAARD, Anker L. HØJBERG a Lars TROLDBORG, 2012. Assessment of hydrological model predictive ability given multiple conceptual geological models. Water Resources Research. 48(6), W06503. ISSN 1944-7973. 10.1029/2011WR011149
SEIFERT, Dorte, Torben O. SONNENBORG, Peter SCHARLING a Klaus HINSBY, 2008. Use of alternative conceptual models to assess the impact of a buried valley on groundwater vulnerability. Hydrogeology Journal. 16(4), 659–674. ISSN 1431-2174, 1435-0157. 10.1007/s10040-007-0252-3
SELROOS, Jan-Olof, Douglas D. WALKER, Anders STRÖM, Björn GYLLING a Sven FOLLIN, 2002. Comparison of alternative modelling approaches for groundwater flow in fractured rock. Journal of Hydrology. 257(1–4), 174–188. ISSN 0022-1694. 10.1016/S0022-1694(01)00551-0
SCHEIBE, Timothy D., Ellyn M. MURPHY, Xingyuan CHEN, Amy K. RICE, Kenneth C. CARROLL, Bruce J. PALMER, Alexandre M. TARTAKOVSKY, Ilenia BATTIATO a Brian D. WOOD, 2015. An analysis platform for multiscale hydrogeologic modeling with emphasis on hybrid multiscale methods. Groundwater. 53(1), 38–56. ISSN 1745-6584. 10.1111/gwat.12179
SIMMONS, Craig T. a Randall J. HUNT, 2012. Updating the debate on model complexity. GSA Today. 22(8), 28–29. ISSN 10525173. 10.1130/GSATG150GW.1
SINGH, Abhishek, Srikanta MISHRA a Greg RUSKAUFF, 2010. Model averaging techniques for quantifying conceptual model uncertainty. Ground Water. 48(5), 701–715. ISSN 0017467X. 10.1111/j.1745-6584.2009.00642.x
TROLDBORG, Lars, Jens Christian REFSGAARD, Karsten Høgh JENSEN a Peter ENGESGAARD, 2007. The importance of alternative conceptual models for simulation of concentrations in a multi-aquifer system. Hydrogeology Journal. 15(5), 843–860. ISSN 1431-2174, 1435-0157. 10.1007/s10040-007-0192-y
UUSITALO, Laura, Annukka LEHIKOINEN, Inari HELLE a Kai MYRBERG, 2015. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environmental Modelling & Software. 63, 24–31. ISSN 1364-8152. 10.1016/j.envsoft.2014.09.017
VAN DER SLUIJS, Jeroen P., Matthieu CRAYE, Silvio FUNTOWICZ, Penny KLOPROGGE, Jerry RAVETZ a James RISBEY, 2005. Combining quantitative and qualitative measures of uncertainty in model-based environmental assessment: the NUSAP system. Risk Analysis. 25(2), 481–492. ISSN 1539-6924. 10.1111/j.1539-6924.2005.00604.x
WAINWRIGHT, John a Mark MULLIGAN, ed., 2013. Environmental modelling: finding simplicity in complexity. 2nd edition. Oxford: Wiley-Blackwell. ISBN 978-0-470-74911-1. environmentalmodelling.net
WALKER, W.E., P. HARREMOËS, J. ROTMANS, J.P. VAN DER SLUIJS, M.B.A. VAN ASSELT, P. JANSSEN a M.P. KRAYER VON KRAUSS, 2003. Defining uncertainty: a conceptual basis for uncertainty management in model-based decision support. Integrated Assessment. 4(1), 5–17. ISSN 1389-5176. 10.1076/iaij.4.1.5.16466
WARMINK, J. J., J. A. E. B. JANSSEN, M. J. BOOIJ a M. S. KROL, 2010. Identification and classification of uncertainties in the application of environmental models. Environmental Modelling & Software. 25(12), 1518–1527. ISSN 1364–8152. 10.1016/j.envsoft.2010.04.011
YE, Ming, Karl F. POHLMANN, Jenny B. CHAPMAN, Greg M. POHLL a Donald M. REEVES, 2010. A model-averaging method for assessing groundwater conceptual model uncertainty. Ground Water. 48(5), 716–728. ISSN 1745-6584. 10.1111/j.1745-6584.2009.00633.x
YOUNG, Peter, 1998. Data-based mechanistic modelling of environmental, ecological, economic and engineering systems. Environmental Modelling & Software. 13(2), 105–122. ISSN 1364-8152. 10.1016/S1364-8152(98)00011-5
a) Z konkurenčních hypotéz by měla být vybrána ta nejméně komplikovaná.
b) Pokud nějaká část teorie není pro dosažení výsledků nezbytná, do teorie nepatří.